The purpose of this final post in my "introduction to Emacs" series
is two-fold: first to introduce a family of programming languages
called Lisp with a focus on a specific implementation called
Emacs-Lisp; then to show you how to use this new language in order
to configure and extend Emacs to do exactly what you want.
If you missed and want to catch-up on the other articles in this series, here are the relative links:
- Part 1/3 - How I use Emacs
- Part 2/3 - The Basics of Emacs
#Whats a Lisp?
If one were to estimate the amount of programming languages developed since computing became a human endeavor, I believe the result would be mind-blowing. I also believe that the rate at which new languages are created and old languages die is relatively high. As a consequence of this, it is safe to say that you've probably never heard, or seen, most programming languages. Because they had such a limited impact on the computing world, there would be no need for you to know about them.
Every programming language implicitly defines a specific model of computation. Most of the languages we use in our everyday activity descent from the C-model, i.e. the model of computation used by the C programming language. This is why you are able to learn C, and then switch to Python with relative little effort: the syntax may change, but the basic concepts needed to know how to read a program remain essentially the same.
Amongst the apparently forgotten programming languages, there are certainly those that have nothing new to teach us. Yet, there are also those which contain deep insights about computing, and which implement profound concepts and ideas. These languages--and the computational model they implicitly describe--I believe are worth understanding, even if we will never use them directly ever again in our everyday programming life. I say this because, as programmers, that is, as problem solvers, its crucial to always remind ourselves that the way we approach a problem is heavily influenced by the tools we use and the languages we write and think in. By becoming aware of different approaches to programming, we increase our general understanding of what can actually be done with computers, which is always a good thing, no matter what.
The more I deepen my understanding about the Lisp model, and the more I can't help but think that languages deriving from this model have something important to tell. While it is certainly not the case that the Lisp model has been completely forgotten, I believe that it is not quite as popular as the more typical C-model, with languages like C, Java, Python, and so on. This is a shame, because Lisp has some incredible ideas which are worth exploring at the very least. Also, something worth noting is that in recent years more and more languages are moving in the direction of the Lisp model.
The original language that later gave rise to the Lisp model was
invented in 1958 by John McCarthy. It was quickly picked-up by AI
researchers because of its orientation towards the manipulation of
symbols, as opposed to numbers, and also because it was much more
flexible than other languages. As time progressed, from the
original Lisp language a series of dialects were born, and so Lisp
became a family of programming language, that is, a baseline model
used to describe computational processes. Each dialect extends the
basic building blocks of the original Lisp model in a particular
direction. The specific dialect we are interested in is called
Emacs-Lisp, also known as elisp, which is the language interpreted
by Emacs. By using elisp we are able to extend and configure Emacs
to work exactly the way we want it to work.
#The Basics of the Lisp Model
Since elisp descends from the Lisp model, it shares a bunch of common building blocks with all the other Lisp languages. These are introduced and discussed in this section.
Observation: All the code reported below can be executed directly
inside Emacs in various ways. For example you can either define an
org-mode source code block, write your code and then press C-c C-c
to execute it, or you can write the code in whatever buffer you
prefer, highlighting the region of the code you want to execute
and then use the function eval-region to actually execute it.
#S-Expressions
The basic expression encountered when writing elisp code is the
S-expression, which is clasically defined in the following
recursive way.
Definition: An S-expression can either be
-
An atom, or
-
An expression of the form
\[(x \phantom{a}.\phantom{a} y)\]
where \(x\) and \(y\) are themselves S-expressions.
;; Some example of S-expressions...
NIL ;; atom (boolean)
t ;; atom (boolean)
foo ;; atom (symbol)
5 ;; atom (integer)
"world" ;; atom (string)
(bar . NIL) ;; expression
(5 . bar) ;; expression
("world" . 5) ;; expression
(5 . (3 . NIL)) ;; expression
(foo . ("world" . NIL)) ;; expression
The notation in which the dot (.) appears is called the dotted-pair notation. Since its very inconvenient to constantly having to write the dot, when actually programming in elisp most of the time another notation, called the list notation, is used instead. It is no wonder then that Lisp stands for "LIst Processor".
(bar . NIL) ;; dotted-pair notation
(bar) ;; equivalent in list notation
(5 . (3 . NIL)) ;; dotted-pair notation
(5 3) ;; equivalent in list notation
("world" . (5 . (bar . NIL))) ;; dotted-pair notation
("world" 5 bar) ;; equivalent in list notation
As we can see, the list notation is essentially the same as the pair-dotted notation, with the removal of the various dots and the NIL atom at the end.
Given an S-expression which consists of a list of elements, which is another way of saying a non-atomic S-expression, the first element of the list is said to be the operator, while the remaining elements are the operands.
Every S-expression has a return value \(v\), which is the atomic element itself, if the S-expression is atomic, or, if the S-expression is a list of elements, is obtained by executing the operator with the given operands. During this execution the expression may also produce other side-effects that can potentially change the global state of the program.
(+ 1 2) ;; returns 3 = 1 + 2
(+ 3 4 5) ;; returns 12 = 5 + 4 + 3
(+ 3 (* 2 2)) ;; returns 7 = 3 + (2 * 2)
(* (+ 1 2) (+ 3 4)) ;; returns 21 = (1 + 2) * (3 + 4)
As you can probably see by now, reading Lisp code does not seem quite the easiest thing to do. In my opinion there are two reasons for this:
-
prefix-notationis used instead of the more commoninfix-notation. This means that instead of having the operator in between the operands, we first write the operator, and then the operands.\[2 + 2 \quad \quad \text{(infix notation)}\] \[+ 2 \quad 2 \quad \quad \text{(prefix notation)}\]
-
Every non-atomic S-expression starts and ends with a parenthesis. This causes some difficulty on the eyes, especially when you have S-expression which contain in themselves other nested S-expressions.
Even though it initially may seem hard, it's actually not that
hard to understand and read Lisp code, once you get used to
it. As a good aid in visualizing the structure of an S-expression
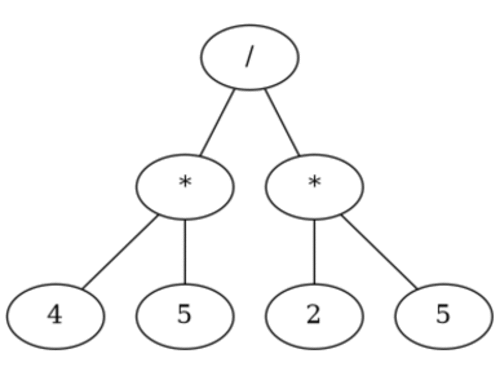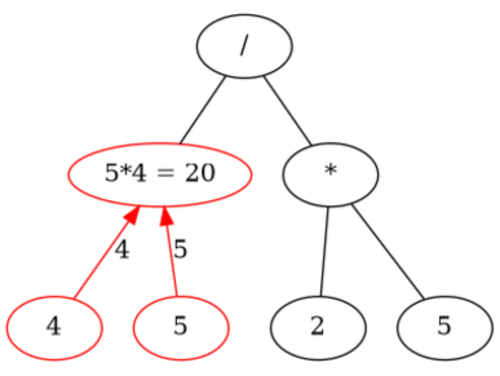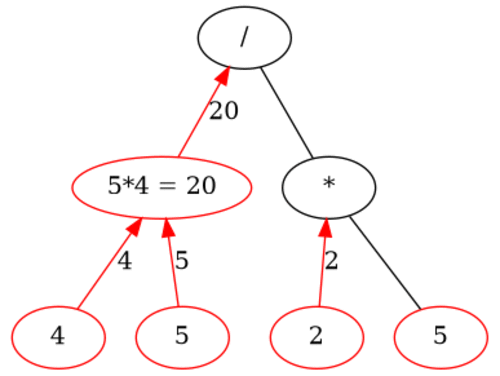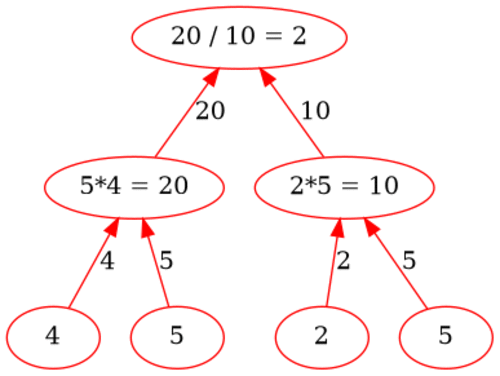
one can use trees. To give an example, the expression (* (+ 1 2) (+ 3 4)) can be visualized with the following tree
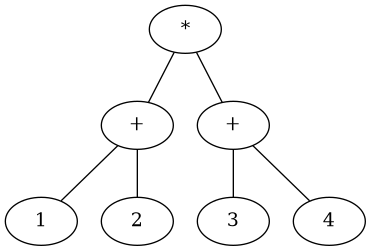
As we can see, the internal nodes are the operators, while the terminal nodes (the leaves of the tree) are the numerals. With this structure in mind computing the value of the entire expression comes down to a process called tree accumulation, in which the values of the terminal nodes are propagated upwards to the internal nodes, which execute their particular operation (for example a sum or a multiplication) and propagate themselves the value obtained to their parent, and so on until the root node is reached and the final value of the expression is computed.
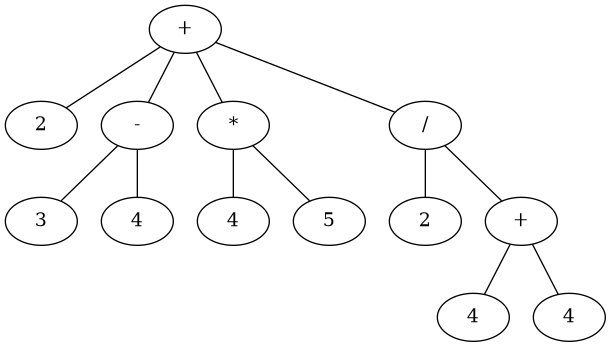
Even what may seem to our untrained human eyes a complicated expressions like
(+ 2 (- 3 4) (* 4 5) (/ 2 (+ 4 4)))
can easily be visualized with a tree as follows
Another way to visualize expression without relying on trees is by aligning the elements which are combined by the same operation, i.e. the elments which in the tree sit on the same level.
(+ 2
(- 3 4)
(* 4 5)
(/ 2
(+ 4 4)))
#Basic Primitives
The main interactions with S-expressions involve the usage of one or more of the following seven primitives.
-
The Quote (') Operator: (quote x)
One of the main characteristic of Lisp which differentiates it from other programming languages, is the fact that the same data structures used to represent the code of the program are also used to represent the data of the program. These data structures are the S-expressions we have just introduced. Reprashing, in Lisp data and code are represented using S-expressions.
To differentiate between an S-expression which represents code and thus has to be processed, and an S-expression which simply represents some data, the quote operator is used in the following way
(quote foo) ;; returns the symbol foo (quote (+ 1 2 3)) ;; returns the symbol (+ 1 2 3) (quote (foo 1 2 (+ 1 2))) ;; returns the symbol (foo 1 2 (+ 1 2))To simplify the syntax, instead of having to write
(quote x)everytime one can simply use the symbol'as the following examples shows'foo ;; equivalent to (quote foo) '(+ 1 2 3) ;; equivalent to (quote (+ 1 2 3)) '(foo 1 2 (+ 1 2)) ;; equivalent to (quote (foo 1 2 (+ 1 2))) -
The Atom Operator: (atom x)
The atom operator returns t (true) if x is an atom or an empty list, while it returns the empty list otherwise.
(atom 1) ;; returns t (atom '()) ;; returns t (atom (+ 1 2)) ;; returns t (atom '(+ 1 2)) ;; returns ()Notice that if we execute
(atom (+ 1 2))we get the resultt, while if we execute(atom '(+ 1 2))we get the empty list(). This is because in the first case the operand(+ 1 2)is seen as a piece of code that has to be executed. When it is executed it produces the value1+2=3, and since3is an atom, the primitive(atom 3)produces the final resultt. In the second case instead the operand'(+ 1 2)is not seen as a piece of code, but rather as simple data. Since'(+ 1 2)is not an atom (it is a list, after all), the primitive(atom '(+ 1 2))produces the final result(). This is exactly what I meant when I said that the'operator allows one to distinguish data from code.Observation: As
Paul Grahamwrote in his article, "The Roots of Lisp" (a must read in my opinion), this quoting mechanism corresponds to the way quotes are used in the English language. Rome is a city in Italy with about 2.8 million people, while "Rome" is a word that contains 4 words. When we add the'we are only considering the syntactical part of the object in question, and we are not interested in its meaning. -
The Eq Operator: (eq x y)
The eq operator returns t if x and y are the same atom or both the empty list, and returns the empty list otherwise.
(eq 1 1) ;; returns t (eq '() '()) ;; returns t (eq 1 2) ;; returns () -
The Car Operator: (car x)
The car operator expects the argument x to be a list, and returns the first element of the list.
(car '(1 2 3 4)) ;; returns 1 (car '("Hello" 2 3 NIL)) ;; returns "Hello" (car '(foo 2 3)) ;; returns foo -
The Cdr Operator: (cdr x)
The cdr operator expects the argument x to be a list, and returns the tail of the list, which is the list from which the first element is removed.
(cdr '(1 2 3 4)) ;; returns (2 3 4) (cdr '("Hello" 3 4 "yo")) ;; returns (3 4 "yo") (cdr '(1)) ;; returns () -
The Cons Operator: (cons x y)
The cons operator expects y to be a list, and returns the list obtained by appending x to y.
(cons 1 '(2 3)) ;; returns (1 2 3) (cons '(1 2) '(3 4)) ;; returns ((1 2) 3 4) (cons "Hello" '(3 4)) ;; returns ("Hello" 3 4) -
The Cond operator: (cond \((p_1 \phantom{a} e_1) \ldots (p_n \phantom{a} e_n)\))
The cond operator is the Lisp way to deal with conditionals, and it works as follows: the interpreter checks the predicate \(p_1\) to see if its true, in which case it executes the expression \(e_1\). If \(p_1\) is false, it checks \(p_2\), and if \(p_2\) is true, it executes \(e_2\). However if also \(p_2\) is false it checks on \(p_3\), and then \(p_4\) and so on until it finds a predicate \(p_i\) that is true, in which case it executes the corresponding expression \(e_i\). The value of the entire cond expression is the value of the specific expression \(e_i\) that is executed.
(cond ((eq 1 2) 3) ((eq 2 2) 4)) ;; returns 4 (cond ((eq '() '()) '(3 4)) ((eq "Hello" "test") '(1 2))) ;; returns (3 4) (cond ((eq '() 2) 2) ((eq 1 2) 3) ('t "Hello World!")) ;; returns "Hello World!"Notice that by putting a predicate of the form
'tat the end of a cond we are making sure that at least the last expression is always executed, since by definition'tis always true.
#Functions Notation
To denote a function the following syntax is used
(defun f (p_1 p_2 ... p_n) e)
where f is the name of the function, the p_1, ... p_n are the
parameters of the function, and e is an expression which denotes
the body of the function.
To understand better how this notation is actually used, the following examples will hopefully help.
-
(square x):
Given an inter value \(x\), the function that computes \(x^2\) can be defined as follows
(defun square (x) (* x x))Once we have defined it, to actually use it we can call with the usual syntax.
(square 10) ;; returns 100 (square 20) ;; returns 400
-
(sum-of-squares x y):
Given two integer values \(x\) and \(y\), the following function will compute the value \(x^2 + y^2\). Notice in the definition we use of the previously defined function
(defun sum-of-squares (x y) (+ (square x) (square y))) (sum-of-squares 10 20) ;; returns 500 (sum-of-squares 5 10) ;; returns 125
-
(factorial n):
Given an integer \(n\), the following function will compute its factorial \(n!\).
(defun factorial (n) (cond ((eq n 1) 1) ;; 1! = 1 ('t (* n (factorial (- n 1)))))) ;; n! = n * (n-1)! (factorial 6) ;; returns 720 (factorial 10) ;; returns 3628800Notice that in the body of the function we recursively call the function.
-
(fibo n):
The Fibonacci numbers form this very famous (and also overly used, at least in CS courses) sequence of numbers
\[1, 1, 2, 3, 5, 8, 11\]
Notice that the first two Fibonacci numbers are both \(1\), and starting from the third one each number is the sum of the previous two. To formalize this sequence we denote \(F_n\) as the \(n\) -th fibonacci number, and we define \(F_1 := 1\), \(F_2 := 1\), and, for any \(n \geq 3\)
\[F_{n} := F_{n-1} + F_{n-2}\]
The following code computes the fibonacci numbers
(defun fibo (n) (cond ((eq n 1) 1) ;; F_1 = 1 ((eq n 2) 1) ;; F_2 = 1 ('t (+ (fibo (- n 1)) ;; otherwise use the formula (fibo (- n 2)))))) ;; F_n = F_{n-1} + F_{n-2} (fibo 5) ;; returns 5 (fibo 10) ;; returns 55 (fibo 15) ;; returns 610The code just given however is not very efficient for all the redudant work it makes. A more efficient version is the following, which proceeds bottom-up using local variables to store the last two fibonacci numbers computed so far in order to get to \(F_n\).
(defun fibo (n) (fibo-iter 1 1 1 n)) (defun fibo-iter (a b count n) (cond ((eq count n) a) ('t (fibo-iter b (+ a b) (+ count 1) n)))) (fibo 15) ;; returns 610 (fibo 50) ;; returns 12586269025 (fibo 100) ;; returns 354224848179261915075
#Other syntax constructs
To finish off our description of the general Lisp model there are some final syntax constructs left to explore. These are are the following:
-
setq
The
setqconstruct is used for variable assignment, and its general syntax is(setq var 1 expr1 var2 expr2 ...)and here follow some examples, to show how its actually used.
(setq foo "bar") (print foo) ;; outputs "bar" (setq name "Leonardo" surname "Tamiano") (print (concat name " " surname)) ;; outputs "Leonardo Tamiano"
-
let
The
letconstruct is used to create a new scope in which local variables can be first assigned, and then used. Its general syntax is(let ((var_1 exp_1) (var_2 exp_2) ... (var_m exp_m)) form_1 form_2 ...)Notice that the values of the various variables are obtained by executing the relative expressions. For example the value of
var_1is given by the result ofexp_1. Once all of the variables have been assigned, the expressions contained in the body of the let construct such asform_1andform_2, can then use those variables for their work. The scope of the variables defined is only limited to the expression inside the body of thelethowever. The value of the entireletexpression is given by the value of the last expression contained in the body.Here is an example to show how its actually used.
(let ((base 2) (height 2)) (/ 2.0 (* base height))) ;; returns 0.5 (/ 2.0 (* base height)) ;; ERROR: variables not found
There is another construct, similar to this one, which is
called let*, and which differs from the let we just discussed
for the fact that the assignments in let* are done
sequentially, while in the standard let the assignemnts are
done in parallel. This allows one to define a variable using a
previously defined variable, like the following example shows
(let* ((base 2)
(height (* base 3))) ;; here I'm using the value of base = 2
(/ 2.0 (* base height))) ;; returns 0.16666666666666666
-
if
Even though we already have the
condconstruct to deal with all sorts of conditional, there is a special construct for the case in which we have anif-or-elsesituation. The general syntax of the construct is the following(if predicate exp1 exp2)where
exp1is the expression that is executed ifpredicatereturnst, and otherwiseexp2is executed. Here is an example to show how its actually used.(if (= 5 5) ;; returns "Yes, 5 is equal to 5!" (print "Yes, 5 is equal to 5!") (print "No, strangely enough 5 is not equal to 5!")) ;; equivalent using cond (cond ((= 5 5) (print "Yes, 5 is equal to 5!")) ('t (print "No, strangely enough 5 is not equal to 5!"))))
-
progn
The
prognallows each of its arguments to be excecuted by the interpreter in a linear sequence, and the value of the entireprognexpression is given by the value of the last expression executed. The general syntax is(progn exp1 exp2 ...)and here follow some example, to show how its actually used.
(progn ;; returns 2 (setq a 2) (print a) )
#How to Extend Emacs Using Elisp
Having introduced the basics of how to read Lisp, we can now dive
deep into using elisp to configure Emacs. The code that will be
presented in this section can be added in the .emacs file that is
either already present in your home directory, or that you can
create it by yourself. This file is read and executed by Emacs
everytime you launch it.
#Packages setup
As we already mentioned, and as I already showed in the first blog post of this series, Emacs is extremely extensible. This means that if you are interested in doing a thing chances are that there is an Emacs package that does that for you. Either that or, with enough time and effort, you can implement it yourself using elisp.
Since dealing with package configuration and package loading is a
problem in and of itself, well, it is no wonder that there is an
emacs package for that. The package is called use-package, and it
is avaiable in the following github repo. To use it simply
download it and add the following to your config file
(add-to-list 'load-path "<path where use-package is installed>")
(require 'use-package)
After that you can set your package-archives with the following code
(use-package package
:config
;; Set priorities of using melpa-stable.
;; The higher the number, the higher the priority.
(setq package-archive-priorities
'(("melpa-stable" . 2)
("MELPA" . 1)
("gnu" . 0)))
;; Add to list melpa stable
(setq package-archives
`(("melpa-stable" . "https://stable.melpa.org/packages/")
("MELPA" . "https://melpa.org/packages/")
("gnu" . "https://elpa.gnu.org/packages/")
))
)
The next time you start Emacs you should be able to execute the
function list-packages to browse through the various packages
offered by Emacs.
The next time you want to install a new package you can simply add it using use-package. Here I will list a bunch of example showing how it works
;; git interface for emacs
(use-package magit
:ensure t ;; make sure its installed
:defer t ;; do not load it immediately
:bind (("C-x g" . 'magit-status)) ;; set keybinds
)
;; package to write DOT files
(use-package graphviz-dot-mode
:ensure t
:config
(setq graphviz-dot-indent-width 4)) ;; code to be executed after the
;; package is loaded
If you want to install a package that is not found in your package archives you can simply download it and add the following code
(add-to-list 'load-path "<path where <package-name> is installed>")
(require '<package-name>)
To deal with this sorts of package I personally have created a
single packages/ directory in which I put all of the things I
have to load at startup. Then with the following code I load all
of them.
;; Iterate over all the files and directories and add them in the load-path
(dolist (package (directory-files "<packages-path>"))
(when (and (not (string= package ".")) (not (string= package "..")))
(add-to-list 'load-path (concat "<packages-path>" package))
)
)
#Basic Customization
To customize the basic appearance and behavior of Emacs the following code can be used.
;; Remove scroll bar
(scroll-bar-mode -1)
;; Remove menu bar
(menu-bar-mode -1)
;; Remove the toolbar
(tool-bar-mode 0)
;; Add column and row number info in the modline
(column-number-mode)
(line-number-mode)
;; Modify the behavior of scroll
(setq scroll-step 3)
;; Remove startup screen
(setq inhibit-startup-screen t)
;; Display Clock
(display-time)
;; Indentation
(setq standard-indent 2)
(setq tab-stop-list nil)
(setq indent-tabs-mode nil)
;; Do not ask to follow symlinks
(setq vc-follow-symlinks t)
#Backup
To manage the way Emacs creates backup files, lockfiles and temporary files, you can check this code.
;; Creates directory for backup files if it does not already exists
(unless (file-exists-p "~/.emacs.d/.auto_saves/")
(make-directory "~/.emacs.d/.auto_saves/")
)
(setq make-backup-files nil ;; do not create backup files
auto-save-default t
auto-save-timeout 1
auto-save-interval 300
auto-save-file-name-transforms '((".*" "~/.emacs.d/.auto_saves/" t))
create-lockfiles nil)
#Keybinds
To set and modify the keybinds the following syntax can be used.
(global-set-key (kbd "C-x t") 'mu4e)
(global-set-key (kbd "C-c e") 'org-encrypt-entry)
(global-set-key (kbd "C-c d") 'org-decrypt-entry)
(global-set-key (kbd "C-=") 'er/expand-region)
As you can see, the idea is to execute the function
global-set-key, with the arguments (kbd <keybind>), and the
quoted name of the function you want to set a keybind for.
#Extension-Mode Association
The following code is used to associate a particular file extension with a particular major-mode, so that everytime we open a file that has that particular extension, Emacs goes immediately on the associated major-mode.
;; Set the association between modes and extensions
(setq auto-mode-alist
(append
'(("\\.cpp$" . c++-mode)
("\\.c$" . c++-mode)
("\\.txt$" . indented-text-mode)
("\\.emacs$" . emacs-lisp-mode)
("\\.gen$" . gen-mode)
("\\.ms$" . fundamental-mode)
("\\.inc$" . asm86-mode)
) auto-mode-alist))
As we can see, once we have added and executed this code,
everytime we open a file with the .c or .cpp extension, Emacs
immediately goes to c++-mode.
#Some Functions
To finish off I will describe some custom functions that I have either wrote myself or found somewhere on the Web.
-
refresh-current-file
This function simply refreshes the current file I'm editing, so that I am able to work on the most recent version of the file.
(defun refresh-current-file() (interactive) (let ( (current-buffer-name (buffer-name (window-buffer (minibuffer-selected-window)))) (current-file-name (buffer-file-name (window-buffer (minibuffer-selected-window)))) ) (kill-buffer-if-not-modified current-buffer-name) (find-file current-file-name) ) )The function is pretty simple: it uses a bunch of emacs variables such as
minibuffer-selected-window, along with other functions such aswindow-buffer,buffer-nameandbuffer-file-name, to get the information I need to know about the buffer I want to refresh. Then it kills the buffer usingkill-buffer-if-not-modifiedand finally it opens again the buffer usingfind-file.Notice in particular the
(interactive)expression at the top of the function. This expression tells Emacs that the function we are defining is an interactive type of function, that is, is a function that can be found usingM-x ENTER refresh-current-file. If we don't put that we woulnd't be able to execute it while editing, nor would we be able to bind it to a particular keybind
Note also that there is another function offered by emacs called
revert-bufferwhich does essentially the same thing (probably even better), so it is not worth to use my specific function. I wanted to include it anyways just to show what is like to write your own elisp function. -
compress-lines
I wrote this other function because I had a problem when editing blocks of text that needed to be indented together. The function works on a region of text, and its effect is to put the entire text in a single line and to replace all the whitespaces in the region with single spaces.
(defun compress-lines (begin end) "replace all whitespace in the region with single spaces" (interactive "r") (save-excursion (save-restriction (narrow-to-region begin end) (replace-string "\n" " ") (goto-char (point-min)) (while (re-search-forward "\\s-+" nil t) (replace-match " ")))))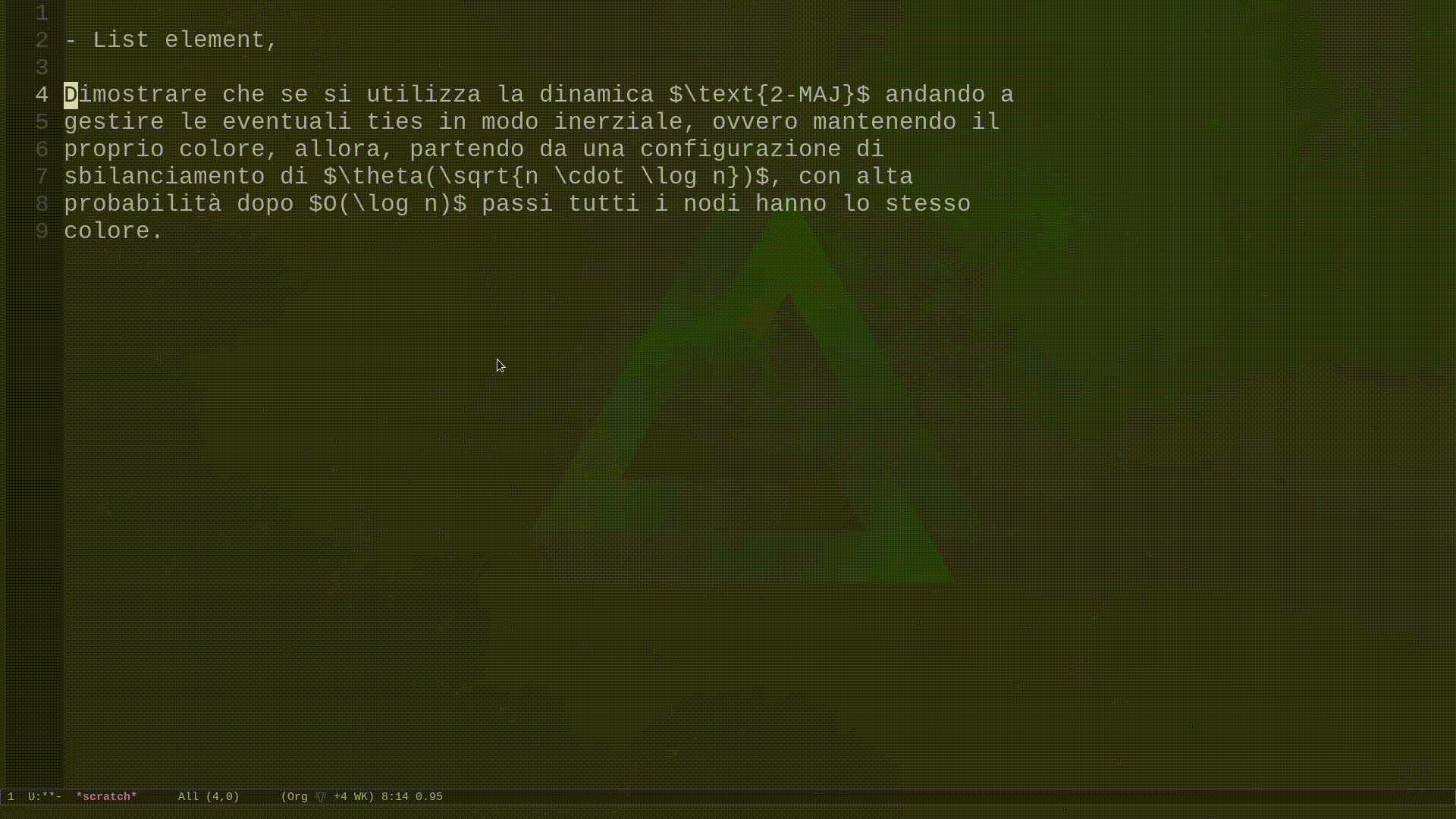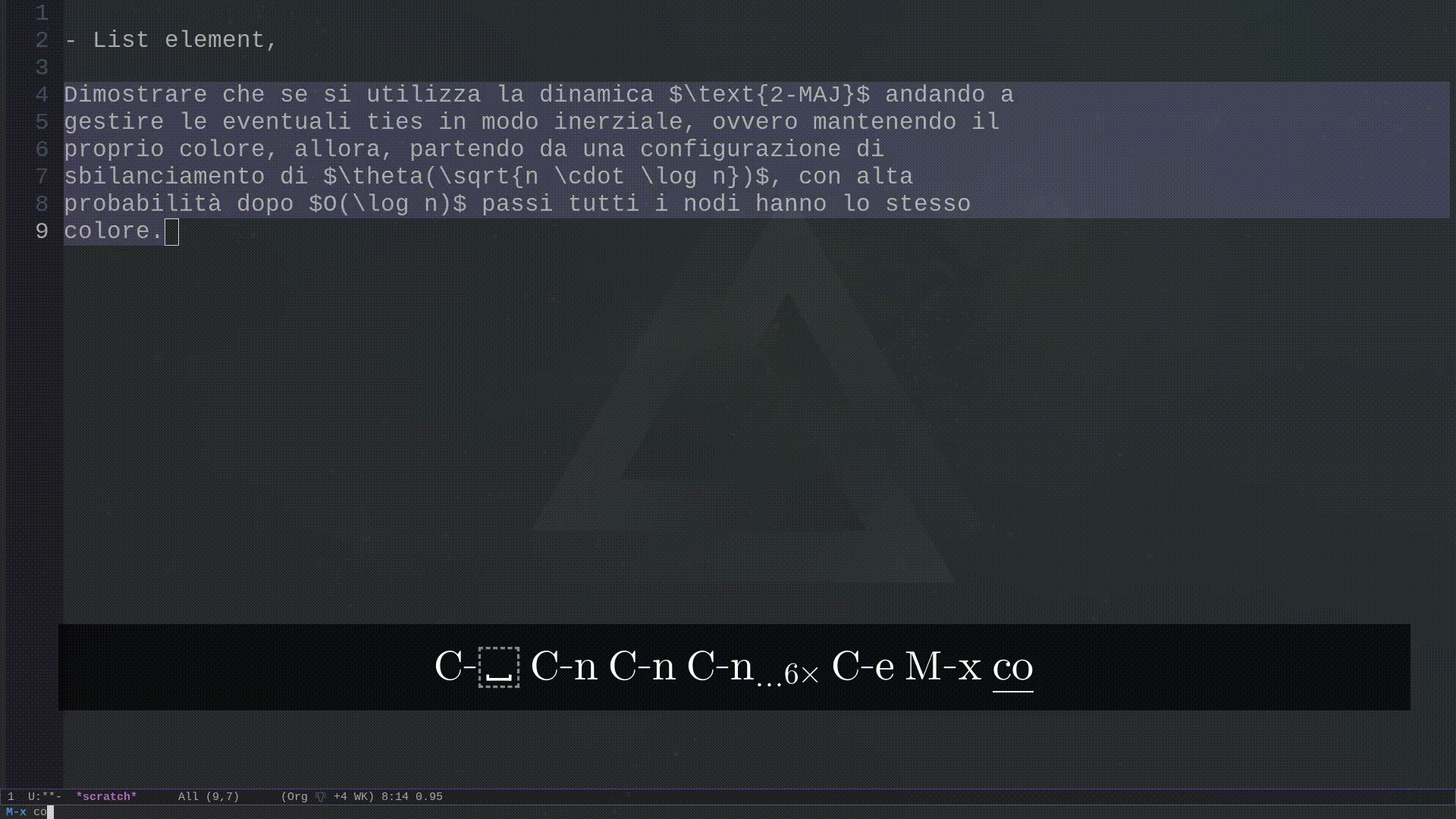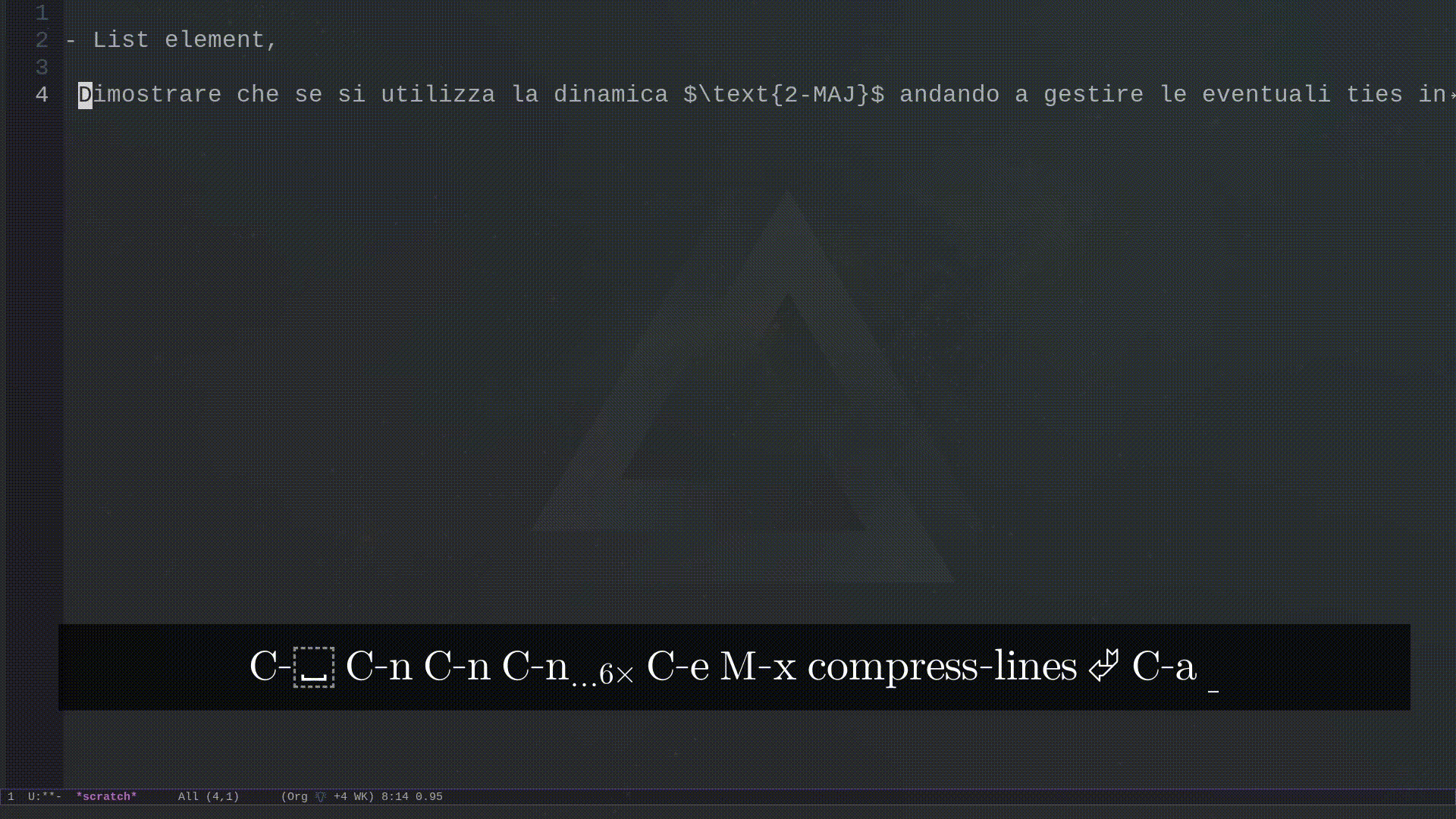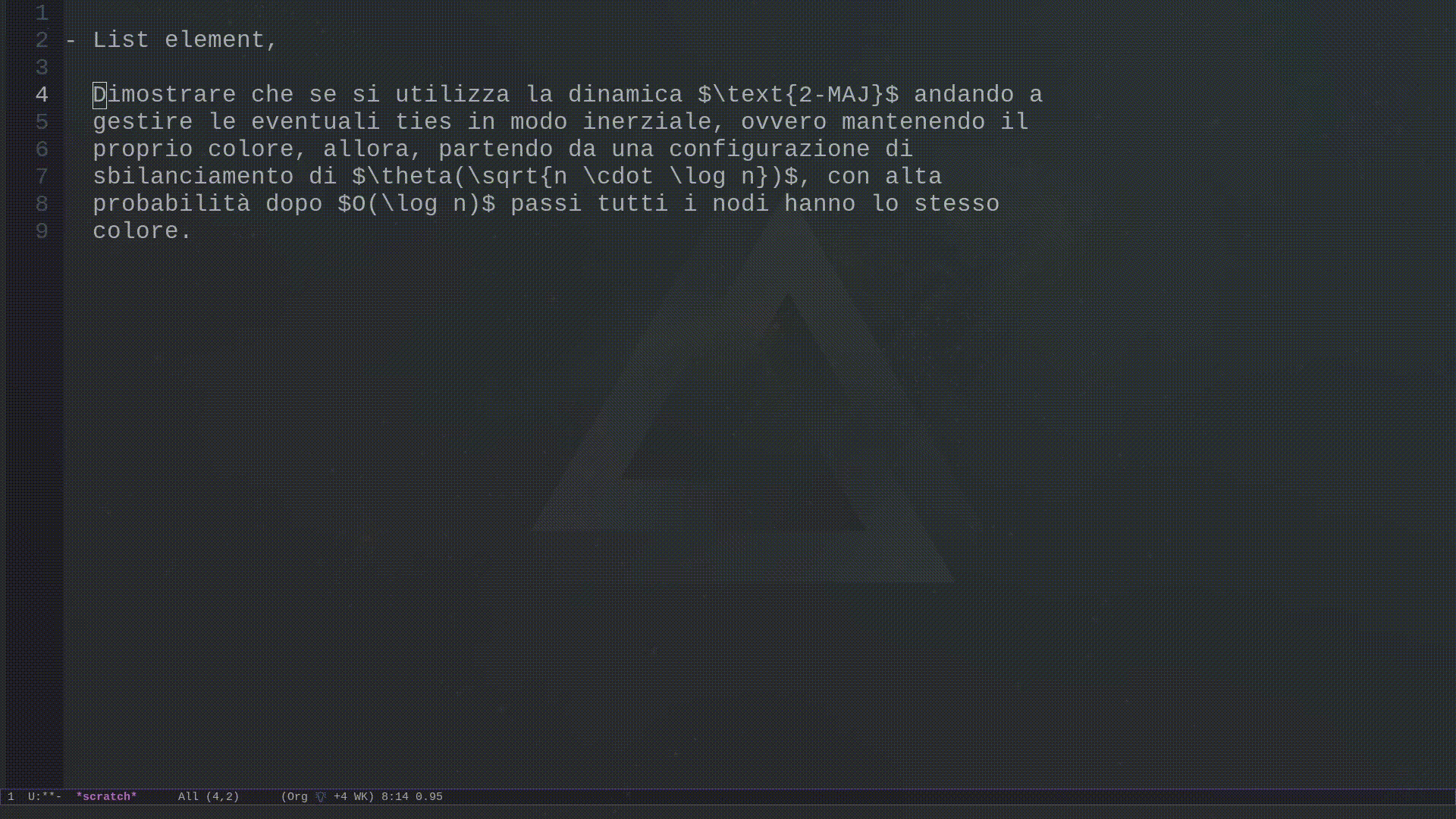
-
my/org-src-block-tmp-window-configuration
This function I did not write myself, but I took it from the following blog post Avoid losing window layout when editing org code blocks. Its purpose is to keep the windows configuration when you are editing a block of source code in org-mode, so that when you finish editing it you get your old layout back.
(defvar my/org-src-block-tmp-window-configuration nil) (defun my/org-edit-special (&optional arg) "Save current window configuration before a org-edit buffer is open." (setq my/org-src-block-tmp-window-configuration (current-window-configuration))) (defun my/org-edit-src-exit () "Restore the window configuration that was saved before org-edit-special was called." (set-window-configuration my/org-src-block-tmp-window-configuration))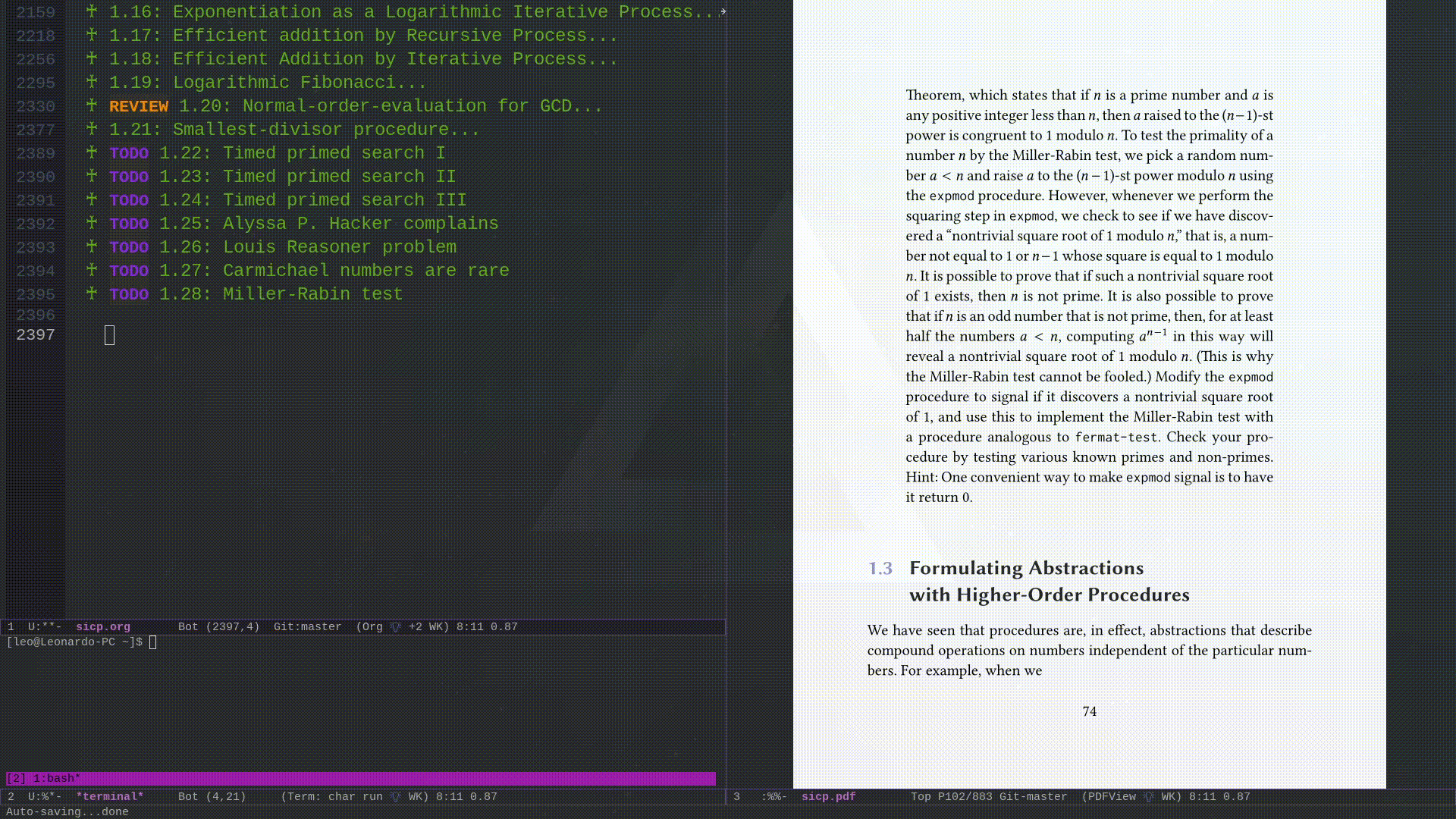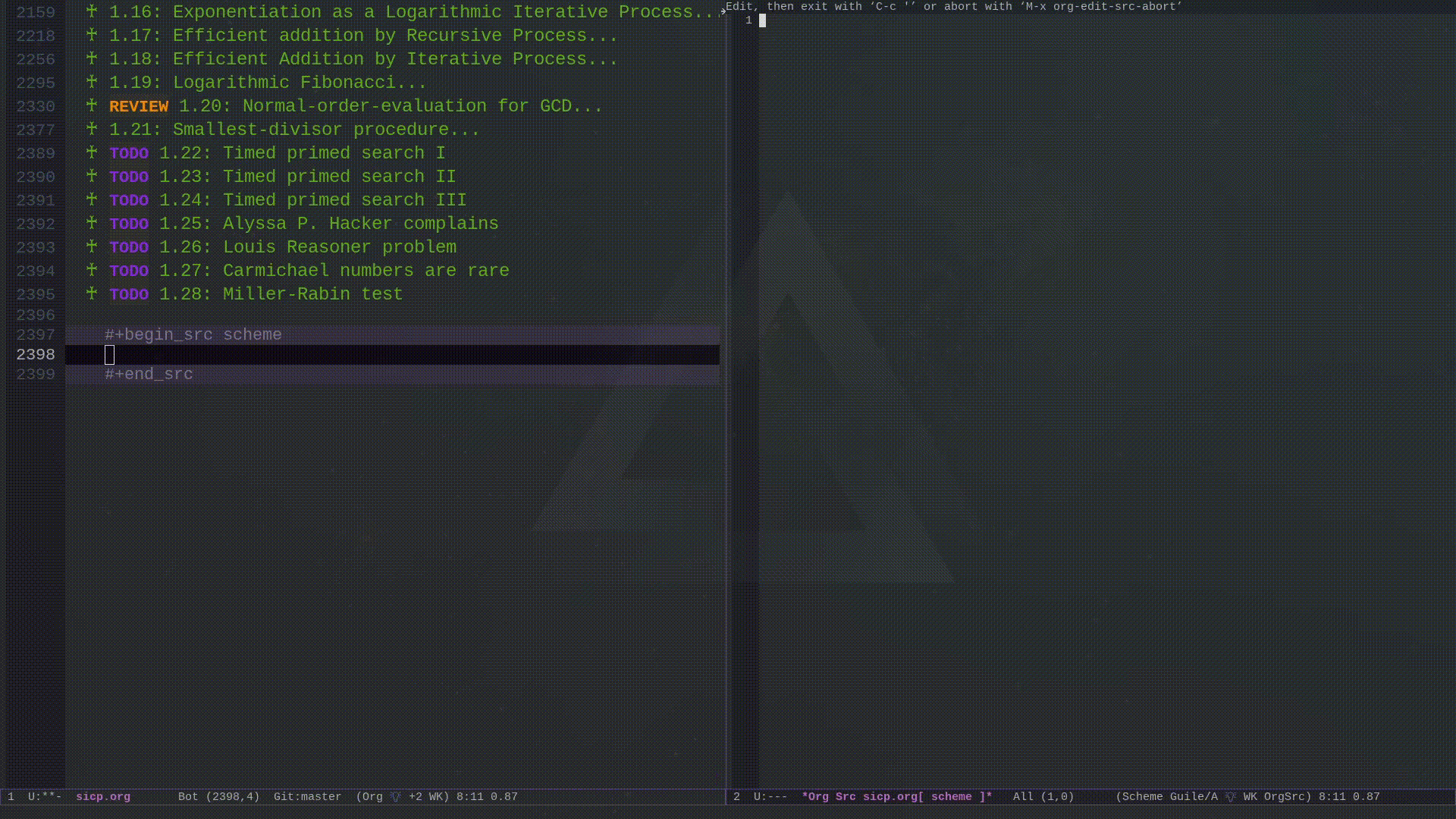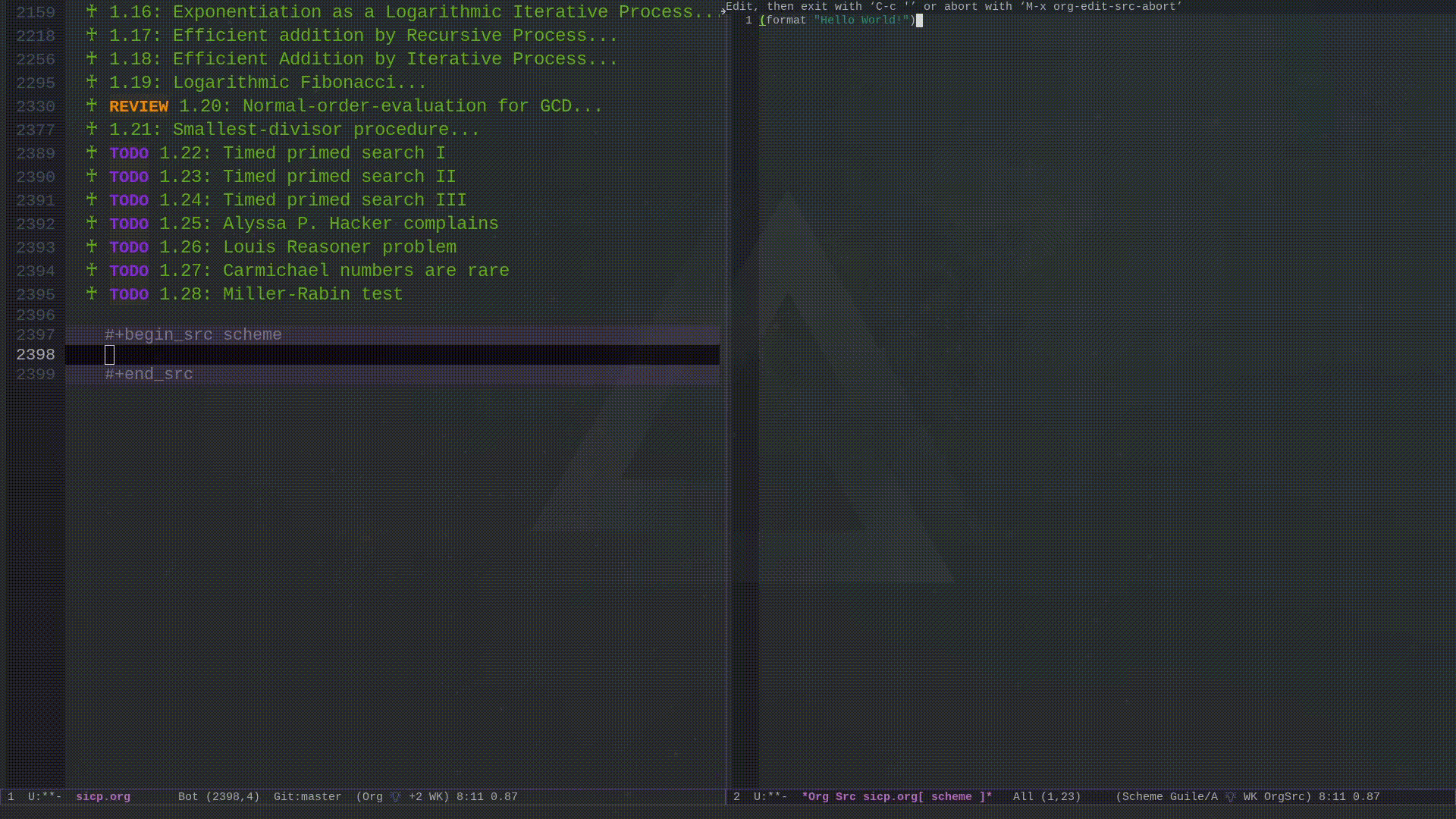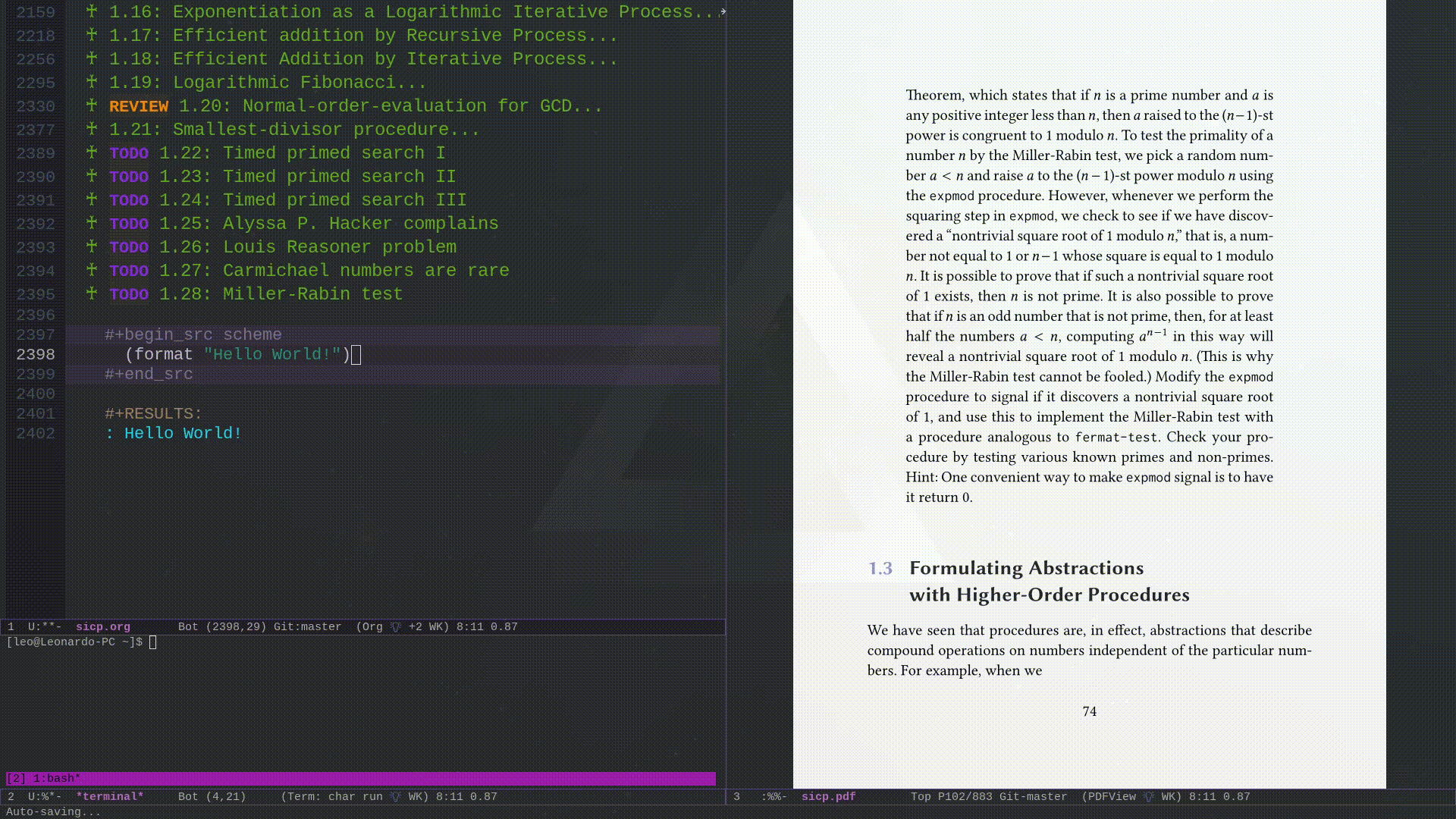
#Now its your turn
At this point you should have a pretty good idea about what Emacs is and what it can do for you. There is a lot left unsaid, but for practical purpose I could not go into every possible detail. Most people don't want to invest the time needed to learn something like this, and its very understandable, since it can be extremely frustrating from time to time to use. However, by having the right mindset, and by understanding that true mastery has a price, you will not just improve your productivity by learning and configuring Emacs to your liking, but you will also have fun while doing so.
Emacs is so big and complex that it really is something more than just a piece of software. Emacs is a framework for thinking. It encompasses an entire universe of possible ideas and workflows, and it has an amazing community made up of people who always try to improve the way they work.
In the last months of my life, Emacs has become one of my greatest source of satisfaction, because the more I learn it, the better I become at it, and the more fun I have while using it. I hope it can help you as well, either by using it directly, or just by knowing and appreciating what are the possibilities offered by technology.
So, I'll leave you to it, and never forget to have fun!
