\(\require{color}\)
Last year I tried to do a PhD in Applied Cryptography. I never
thought I'd end up trying to do a PhD, but that's exactly what
happened. One of the professor I met during my master's taught a
course called Computer and Network Security, which essentially
discussed how to break network protocols and how to design secure
network protocols.
The course was extremely fascinating, also because it was one of the few courses that actually tried to go deep into the subject instead of just giving a general overview. You know those courses that when they explain cryptography they just mention a vague notion of "key" and of "key exchange", and they never really tell you how it is actually done under the hood.
For my master's thesis I asked this professor if he had something for me to work on, and he suggested I'd study the most famous attacks that have been found on the TLS protocol. If you have no idea of what the TLS protocol is and why it exists, I suggest you read one of my previous blog post, where I explain exactly what it is. You can find it in the URL below.
Even though few months ago I dropped out of my PhD program, as it was not working for me, I'm still deeply fascinated by certain ideas and certain cryptographic attacks.
In this blog post I want to talk about one of these attacks that
hooked me right from the beginning. What fascinated me the most
about this attack is the underlying interaction between computer
science and mathematics that it showcases. The attack is known in
the research community as the Bleichenbacher's Padding Oracle named
after the researcher who found it in 1998, Daniel Bleichenbacher. You can find the original article detailing the
attack in the URL below
https://archiv.infsec.ethz.ch/education/fs08/secsem/bleichenbacher98.pdf
The paper is called
Chosen Ciphertext Attacks Against Protocols Based on the RSA Encryption Standard PKCS #1
This is one of those cases where the paper title describes, quite literally, what you will find in the article itself. I really like these titles. While they do not catch the attention of the generalist, for the specialist who knows what to look for it is quite useful to have such information-dense titles.
As the title says, the attack is a choosen cipher attack, which attacks RSA ciphers when used with a specific padding scheme known as PKCS #1v1.5. I will now describe the intuition behind the attack, and then I will enter into some technical details on all the components needed to understand the whole attack.
#Some Intuition First
Suppose there is a client and a server that are interacting with eachothers. In order to protect their communication, client and server perform a protocol which allows them to first generate a symmetric key, and then to share it with eachothers.
The protocol could work as follows:
-
The server has generated its own public and private RSA key pair \((N, e, d)\)
-
The client knows the public key of the server \((N, e)\)
-
The client generates a random symmetric key \(k\)
-
In order to share the key \(k\) with the server, the client encrypts this key with the public RSA key of the server. That is, the client computes the value
\[a := k^e \mod N\]
The value \(a\) is then sent into an unprotected channel.
Now, if you remember your RSA, then you know that assuming the size of the server's public key is around \(2048\) to \(4096\) bits, then it is highly unlikely that a malicious actor, by observing the value \(a\) sent, is able to reverse the exponentiation and obtain the symmetric key \(k\). To do that would be equivalen to compute the private key \(d\), as we know from RSA that
\[\begin{split} a^d &= (k^e)^d \mod N \\ &= k^{(e \cdot d)} \mod N \\ &= k^1 \mod N \\ &= k \mod N \end{split}\]
Well, the Bleichenbacher's Padding Oracle allows a malicious attacker to actually decrypt the value \(a\) without knowing the private key \(d\). This doesn't break our current knowlede of mathematics, because what happens in this attack is actually very practical. Instead of finding a smart way to bypass the computational complexity of factoring, this attack abuses a particular scenario in which the server might find himself in.
Before I mentioned that the client sends in the unprotected channel the value of \(a\), where \(a\) was obtained through a vanilla computation of RSA. Since using this form of "Vanilla RSA" can cause many other problems, a padding scheme is needed. Padding schemes do not come as a result of research in mathematical beauty. They come out for extremely practical reasons. It so happens that when it comes to RSA, a well known and standardized padding scheme is the PKCS#1v1.5 scheme, introduced in RFC XXXX.
This means that the client actually does not send in the unprotected channel the value of \(a\). Before encrypting the message \(k\), it first pads it according to PKCS#1v1.5 rules, and only then it encrypts the value using the RSA public key. This means that now the process client-side looks as follows
\[k \rightarrow \texttt{PKCS#1v1.5}(k) \rightarrow \bigg(\texttt{PKCS#1v1.5}(k)\big)^e \mod N\bigg)\]
From the plaintext message we want to protect \(k\), we first pad it to obtain \(\texttt{PKCS#1v1.5}(k)\) and then we encrypt it. Finally, we send this encrypted value into the unprotected communication channel.
This means that server-side the processing will be different too, as we have to account for this extra padding step. In particular the server will have to "unwrap" the value as follows.
\[\begin{split} \bigg(\texttt{PKCS#1v1.5}(k)\big)^e \mod N\bigg) &\rightarrow \bigg(\texttt{PKCS#1v1.5}(k)\big)^e \mod N\bigg)^d \\ &\rightarrow \texttt{PKCS#1v1.5}(k) \\ &\rightarrow k \\ \end{split}\]
The server receives the encrypted padded message. The first thing it does, is it uses its own private key to decrypt the message in order to obtain the original padded message. Finally, it unpads the message in order to obtain the original plaintext message \(k\).
Now, what happens if, after the decryption step, the server realizes that the message obtained from the decryption is not properly padded with respect to PKCS#1v1.5? One could say, simple, just tell your user.
[ERROR]: Hey, your message is not properly PKCS#1v1.5 padded!
Now, if you actually do this, then you enable the attack to work. Indeed, by sending maliciously crafted ciphertext messages, an attack can use this simple information – whether the decrypted message is properly padded or not – to actually decrypt an encrypted message of choice. Say, for example, the initial message sent by the client to the server containing the symmetric key. The attacker just needs to store somewhere this message, and by asking many such questions to the server, the attacker is able to figure out the original plaintext message value.
This might seem weird and, I hope, also cool and amazing. Because it is all of those things. As I said, in this attack multiple layers of human knowledge come into play, from the more practical one, such as padding schemes, to the more abstract and beautiful ones, such as the mathematics behind RSA.
So, to recap, let me go over it once again, just to make sure you understand.
If we have a server, any server, that exposes an interface to receive PKCS#1v1.5 padded messages, and if the server tells us clearly if a message it has received is properly padded or not, then we can launch an attack which, after a certain amount of queries, allows us to use the server's key to decrypt a message of our choice, whathever the message is, as long as it was encrypted with the same key that the server uses to decrypt the incoming messages.
#Technicalities
At this point, given that we have a useful overview of the attack, we can start going into the depth of the attack itself. To fully understand the attack we will need to review the following:
-
How encryption/decryption works in RSA.
-
What is a valid padding according to PKCS#1v1.5.
-
The idea of a padding oracle.
Let's go in order then.
#1 – RSA
RSA is one of the first public cryptosystems discovered and implemented that can be used for both encryption – to grant confidentiality – and for digital signatures – to grant integrity. With the external help of the Public-Key-Infrastructure (PKI) it can also be used to grant authentication.
In RSA the process of generating a new key works as follows:
-
Two "big" primes \(p\) and \(q\) are choosen by the user that wants a new key.
-
Then, out of those two primes, the folowing numbers are computed
\[\begin{split} N &= p \cdot q \\ \phi(N) &= (p-1) \cdot (q-1) \\ \end{split}\]
where \(\phi(N)\) is Euler's totient function.
-
After that, an exponent \(e < \Phi(N)\) is choosen from the modular group \(\mathbb{Z}_{\Phi(N)}\) such that \(e\) is coprime with \(\Phi(N)\).
-
Finally, an exponent \(d\) also beloging to the modular group \(\mathbb{Z}_{\Phi(N)}\) is computed by inverting the previously choosen element \(e\).
At the end of the key generation process in RSA we have the following parameters:
\[p \;\;,\;\; q \;\;,\;\; N \;\;,\;\; \Phi(N) \;\;,\;\; e \;\;,\;\; d\]
Out of all these parameters the couple \((N, e)\) form the public set of parameters for an RSA key, while \(d\) is the private key.
Encryption and decryption are then implemented as modular exponentiation. The only difference between the two operations is the exponent used.
-
For encryption we use the public exponent \(e\)
\[c = m^e \mod N\]
-
For decryption we use the private exponent \(d\)
\[m = c^d \mod N\]
RSA works because of the following property, which is a consequence of Euler's Theorem
\[m^{e \cdot d} \mod N = m^1 \mod N = m \mod N\]
Out of the various properties of RSA, the most crucial one to understand in the context of the Bleichenbacher's Oracle is the property of malleability, which is a consequence of the fact that encryption and decryption are implemented through modular exponentiation.
The RSA cryptosystem is said to be malleable.
This means that given an encrypted text \(c = m^e \mod N\) and a public key \((e, N)\), we can create a new, valid cipertext by computing
\[s^e \cdot c \mod N\]
where \(s\) is an arbitrary positive number.
This new value is a valid ciphertext, since
\begin{equation*} \begin{split} s^e \cdot c \mod N &= s^e \cdot m^e \mod N \\ &= (s \cdot m)^e \mod N \\ \end{split} \end{equation*}
As we can see, the new plaintext associated with this new ciphertext is \(s \cdot m\). This means that, not only starting from any valid ciphertext in RSA we can construct arbitrary many other valid ciphertexts. We also know the exact relationship between the plaintext of the original valid ciphertext, \(m\) in our case, and the plaintext of the new constructed ciphertext, \(s \cdot m \mod N\).
This leaves open the possibility for a choosen ciphertext attack, where an attacker is able to send to the server maliciously crafted yet valid ciphertext messages.
#2 – PKCS#1v1.5
Consider we want to transmit a message protected with RSA encryption, where we know the public parameters \((e, N)\) of the receiver. The idea is to start from the message bytes and construct a particular number \(m \in [0, N]\).
\begin{equation*} \begin{split} \text{Message bytes} &\longrightarrow \text{Padding bytes + Message bytes} \\ &\longrightarrow m \in [0, N) \end{split} \end{equation*}
The number will be generated using randomness so that if we encrypt multiple times the same message bytes we will get different ciphertexts.
Let us assume that \(k\) is the byte-length of \(N\). The padding scheme defined for encryption by the standard \(\texttt{PKCS#1v1.5}\) can be described as follows:
-
The first two bytes are set to \(\texttt{0x00}\) and \(\texttt{0x02}\).
-
Then at least \(8\) random bytes different from \(\texttt{0x00}\).
-
Then a single null byte \(\texttt{0x00}\).
-
Finally the remaining bytes are the message's byte.
Schematically we get,
\[ \texttt{0x00 0x02} \;\; | \;\; \underbrace{RB_1 \; \ldots \; RB_i}_{\geq 8} \;\; | \;\; \texttt{0x00} \;\; | \;\; MB_1 \; \ldots \; MB_j\]
where \(RB_i\) are random bytes and \(MB_j\) are message bytes.
Notice that from the second constraint it follows that with this padding scheme we can have at most \(k-11\) application data bytes per packet. In case the message is longer than that, the idea is to split the message in multiple packets and encrypt each one. Then the receiver will decrypt each packet, extract the data bytes from the various packets, and append them together to get back the message bytes.
Putting it all together, we get
\begin{equation*} \overbrace{\texttt{0x00 0x02} \;\; | \;\; \underbrace{RB_1 \; \ldots \; RB_i}_{\geq 8} \;\; | \;\; \texttt{0x00} \;\; | \;\; \underbrace{MB_1 \; \ldots \; MB_j}_{\leq k - 11}}^k \end{equation*}
#3 – Padding Oracles
To understand the Bleichenbacher's Padding Oracle Attack and many other type of attacks done to TLS over the years, it is important to understand the idea behind a padding oracle.
One of the first usage of the concept of an oracle can be found in
Alan Turing PhD thesis of 1938, in which he states
Let us suppose we are supplied with some unspecified means of solving number-theoretic problems; a kind of oracle as it were. We shall not go any further into the nature of the oracle apart from saying it cannot be a machine
as we can intuitively understand from the given description, an oracle can be thought of as an abstraction that lets us answer specific questions. Different oracles are able to answer for different questions, but the general idea is that when using an oracle, we are not really interested in how the oracle comes up with the answer; we're only interested in the output of the oracle. We abstract the question, and we assume to have a black-box opaque mechanism that is able to answer our question with a well defined precision, which can either be totally determinstic or also probabilistic.
The Bleichenbacher's Oracle Attack is based on the following oracle:
Let \(h_{(e, N)}\) be a function that takes in input a ciphertext \(c = m^e \mod N\) encrypted with a specific RSA public key \((e, N)\) and outputs True is the plaintext \(m\) is a valid, \(\texttt{PKCS#1v1.5}\) conforming plaintext, and False otherwise.
This oracle can be used to understand if a given ciphertext, when decrypted, decrypts to a valid \(\texttt{PKCS#1v1.5}\) plaintext, that is a plaintext that follows the rules of the padding scheme.
In our particular discussion about the Bleichenbacher Attack, we assume to be working with an oracle that only checks the first two bytes of the message. If, given an encrypted message \(c\), the decryption process obtains a plaintext \(m\) that starts with the bytes \(\texttt{0x00}\) \(\texttt{0x02}\), then the plaintext is deemed to be \(\texttt{PKCS#1v1.5}\) conforming and the oracle returns True. Otherwise, the plaintext is not properly padded, and the oracle returns False.
The following python code implements the oracle just described
def oracle(msg_hex):
# assume we know private key from global context
global D, N
# transform hex into number
encrypted_msg = int("0x" + msg_hex, 0)
# raw decrypt using RSA
decrypted_msg = pow(encrypted_msg, D, N)
decrypted_hex = f"%0{PADDING_VALUE}x" % decrypted_msg
# check for padding
if decrypted_hex[0:4] != "0002":
return False
else:
return True
#The Attack
The Bleichenbacher attack is an adaptive choosen ciphertext attack which uses a cryptographic oracle based on RSA and \(\texttt{PKCS#1v1.5}\) to decrypt a message \(c\) which was encrypted using the public key of the server we're trying to attack.
The attack is based on the following things:
-
In RSA both plaintext and ciphertext are numbers.
-
Satisfying all padding rules of \(\texttt{PKCS#1v1.5}\) puts heavy contraints on the numerical range the plaintext can belong to.
-
The malleability of RSA allows an attacker to create new ciphertexts whos plaintexts can be related to the original plaintext.
Let \(m\) be a message padded with PKCS #1 v1.5, and let \(c\) be its encrypted form. Our objective is to find the original \(m\).
NOTE: The attack can still be done if \(m\) is any message (even not correctly padded), but it requires an additional starting phase which we'll briefly cover at the end.
#Consequences of PKCS #1 v1.5
If we remember how the padding standard PKCS #1 v1.5 was defined, we'll recall that all messages that satisfy this padding scheme start with the byte sequence \(\texttt{0x00 0x02}\).
Let \(k\) be the size in byte of the modulus \(N\), where \(N\) is part of the public key of the server. By defining
\[B = 2^{8 \cdot(k - 2)}\]
we have that
\[\begin{split} B &\longrightarrow \text{0x 00 01 } \overbrace{\text{00 00} \ldots \text{00}}^{k - 2 \text{ bytes}}\\ 2B &\longrightarrow \text{0x 00 02 } \text{ 00 00} \ldots \text{00} \\ 3B &\longrightarrow \text{0x 00 03 } \text{ 00 00} \ldots \text{00} \\ \end{split}\]
This means that
\[2B \leq m \leq 3B - 1\]
Notice how satisfying \(\texttt{PKCS#1v1.5}\) padding rules puts heavy contraints on the numerical range the plaintext can belong to.
#Decryption Algorithm
The decryption algorithm works in various phases, where each phase is indexed by a natural number \(i \in \mathbb{N}\) and contains two steps.
-
The first step tries to find a value \(s_i\) such that
\[s_i \cdot m \mod N\]
is \(\texttt{PKCS#1v1.5}\) compliant.
-
The second step constructs, starting from the \(s_i\) discovered previously, a set of intervals \(M_i\) such that
\[\exists [a, b] \in M_i: \;\; m \in [a, b]\]
The idea is that at each step we're reducing the length of the intervals belonging to \(M_i\), to arrive at a point where there is only a single interval in \(M_i\) which contains only a single number: that number will be our plaintext.
Initialization phase: \(i = 0\)
At the start we initialize the following values
\[\begin{split} s_0 &= 2 \\ & \\ M_0 &= \{\;\; [2B, 3B] \;\;\} \\ \end{split}\]
Generic phase: \(i \in \mathbb{N}^+\)
Step 1 – Search for next \(s_i\)
We start from \(s_i = s_{i-1} + 1\) and find the next value such that
\[s_i \cdot m \mod N\]
is \(\texttt{PKCS#1v1.5}\) compliant. If a given \(s_i\) does not work, we try the next \(s_i = s_i + 1\). To test a given \(s_i\) we send to the oracle the following value
\[s_i^e \cdot c \mod N\]
If the oracle replies with "YES", then we stop and go to the next step. Otherwise we keep going check for the next value of \(s_i\). The code for this phase is
def bleichenbacher_step_1(s):
global E, N, TOTAL_REQUESTS
s = s + 1
while True:
new_ciphertext = (pow(s, E, N) * ENCRYPTED_FLAG) % N
encrypted_hex = f"%0{PADDING_VALUE}x" % new_ciphertext
if oracle(encrypted_hex) == True:
return s
s = s + 1
TOTAL_REQUESTS += 1
Step 2 – Construction of M_i
We already saw that if \(s_i \cdot m \mod N\) is \(\texttt{PKCS#1v1.5}\) compliant, then
\[2B \leq s_i \cdot m \mod N \leq 3B - 1\]
For how we define the modulus operation, this means that there exists a \(k \in \mathbb{Z}\) such that
\[2B \leq s_i \cdot m - k \cdot N \leq 3B - 1\]
Summarizing,
- \(s^e \cdot c \mod N\) is accepted by the oracle.
- \(s \cdot m \mod N\) is PKCS #1 v1.5 compliant.
- \(2B \leq s \cdot m \mod N \leq 3B - 1\)
- \(\exists k \in \mathbb{Z}: \;\; 2B \leq s \cdot m - k \cdot N \leq 3B - 1\)
From (4) we get
\[\begin{split} \frac{2B + k \cdot N}{s_i} \leq m \leq \frac{3B - 1 + k \cdot N}{s_i} \end{split}\]
Even though this represents a new bound for \(m\), which can potentially give us new information on the plaintext message, the problem here is that we cannot use directly this range, as we do not know the value of \(k\) in the previous equation and so we cannot compute the edges of the interval.
To solve this problem the idea is that since the values of \(s_i\) and \(m\) are fixed, we can enumerate all possible values of \(k\)
\[2B \leq s_i \cdot m - k \cdot N \leq 3B - 1\]
\(\implies\)
\[\frac{-3B + 1 + s_i \cdot m}{N} \leq k \leq \frac{-2B + s_i \cdot m}{N}\]
In particular, from the initial bound \(m \in [2B, \;\; 3B - 1]\) we have that
\[\frac{-3B + 1 + s_i \cdot \textcolor{red}{2B} }{N} \leq \frac{-3B + 1 + s_i \cdot \textcolor{red}{m}}{N} \leq k \leq \frac{-2B + s_i \cdot \textcolor{blue}{m}}{N} \leq \frac{-2B + s_i \cdot (\textcolor{blue}{3B - 1})}{N}\]
Thus, for each value of \(k\) taken from the interval
\[\frac{-3B + 1 + s_i \cdot 2B}{N} \leq k \leq \frac{-2B + s_i \cdot (3B - 1)}{N}\]
we have a new possible interval for \(m\)
\[\frac{2B + k \cdot N}{s_i} \leq m \leq \frac{3B - 1 + k \cdot N}{s_i}\]
Since they are disjoint intervals, out of all them, the original plaintext \(m\) only belongs to one of them, the one associated to the value of \(k\) which makes (4) true. Given however that we don't know the particular \(k\), we proceed by
More generally, let's say we're on the second step of round \(i\). This means that in the previous round we've computed the set of intervals \(M_{i-1}\). The plaintext \(m\) belongs to one such interval, but we don't know which. The objective for this step is to compute \(M_i\) by using the \(s_i\) found before.
For each \([a, b] \in M_{i-1}\) we obtain the following range for \(k\)
\[\frac{-3B + 1 + s_i \cdot \textcolor{red}{a}}{N} \leq k \leq \frac{-2B + s_i \cdot \textcolor{blue}{b}}{N}\]
and for every value in this range we get a new possible interval for \(m\)
\[\frac{2B + k \cdot N}{s_i} \leq m \leq \frac{3B -1 + k \cdot N}{s_i}\]
A new interval \([aa, bb]\) is added to \(M_i\) if and only if it has a non-empty intersection with \([a, b] \in M_{i-1}\), where
\[[aa, bb] = \Bigg[\frac{2B + k \cdot N}{s_i}, \;\; \frac{3B -1 + k \cdot N}{s_i}\Bigg]\]
To compute these intersection the max and min functions are used. This is the idea behind the main formula of the decryption algorithm found in the original paper (in the paper \(k\) is writtne as \(r\), the rest is the same)
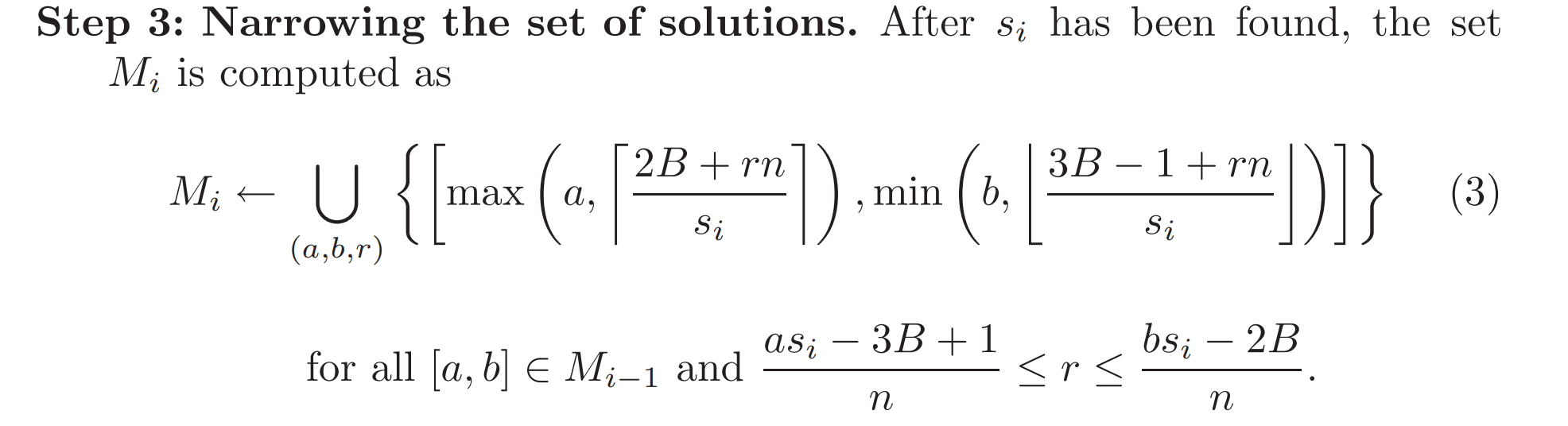
Once again a key point to stress is that at every iteration the only thing we know for certain about the new set of intervals \(M_i\) is that \(m\) belongs to a single interval of \(M_i\), even though we cannot tell which. This is the main invariant of the algorithm, which can be used with an inductive argument to prove its correctness. In formula we can write
\[\exists [a, b] \in M_i: \;\; m \in [a, b]\]
At the end of this second step for the phase \(i\), if the set \(M_i\) contains a single interval, and if this interval is of the form \([a, a]\), then we can stop, since
\[m \in [a, a] \implies a \leq m \leq a \implies m = a\]
If instead \(M_i\) contains one or more intervals, or if it contains a single interval of the form \([a, b]\), with \(a \neq b\), then the algorithm proceeds towards the next phase \(i + 1\) as described previously.
The code for this second step is reported below
def bleichenbacher_step_2(s, old_M):
new_M = set([])
for (a, b) in old_M:
r1 = ceil((a * s - B3 + 1), N)
r2 = floor((b * s - B2), N) + 1
for r in range(r1, r2):
aa = ceil(B2 + r*N, s)
bb = floor(B3 - 1 + r*N, s)
newa = max(a, aa)
newb = min(b, bb)
if newa <= newb:
new_M |= set([ (newa, newb) ])
return new_M
#Initial Optimizations
The algorithm just described in theory already works. In practice however it is just too slow. To overcome this problem the original paper defined the algorithm with the following two optimizations. These steps do not change the logic of the attack, they just increases its performance.
-
At the start, instead of starting from \(s_0 = 1\), we start with
\[s_0 = \left \lceil \frac{N}{3B} \right \rceil\]
-
If at the end of phase \(i\), the set \(M_{i}\) contains a single interval \([a, b]\), then we optimize the search for the next \(s_{i+1}\) by using a heuristic.
The first optimization is a direct consequence of the fact that for value of \(s_0 \leq \left \lceil \frac{N}{3B} \right \rceil\) it is simply not possible to have a PKCS compliant plaintext. Indeed,
\[k \leq \frac{m_0 \cdot s_1 - 2B}{N} \leq \frac{(3B - 1) \cdot s_1 - 2B}{N} < \frac{3B s_1}{N}\]
Such value is \(1\) when \(s_1 = \frac{N}{3B}\). If \(s_1 < \frac{N}{3B}\), then \(k < 1 \implies k = 0\). In these cases
\[m_1 = m_0 \cdot s_1 - k \cdot N = m_0 \cdot s_1 < N\]
and so we can't respect PKCS padding, since the value will never start with \(\texttt{0x00}\) \(\texttt{0x02}\).
The second optimization instead is based on a heuristic. The general idea is to have that the next value of \(s_{i+1}\) is, approximately, double the previous value. In formula,
\[s_{i+1} \approx 2 \cdot s_{i}\]
In detail, if \(M_{i} = \{\;\; [a, b] \;\; \}\), then we let
\[r_i \geq 2 \cdot \frac{b \cdot s_i - 2B}{n}\]
and we start to try all \(s_{i+1}\) in the following interval
\[\frac{2B + r_i \cdot n}{b} \leq s_{i+1} \leq \frac{3B + r_i n}{a}\]
until \(s_{i+1}^e \cdot c \mod N\) is accepted by the oracle. If the interval
\[\frac{2B + r_i \cdot n}{b} \leq s_{i+1} \leq \frac{3B + r_i n}{a}\]
finishes without finding any valid \(s_{i+1}\), then we increment \(r_i = r_i + 1\) and we start the search for the next \(s_{i+1}\) in the new interval. Notice that if the value \(s_{i+1}\) works, then we have
\[\begin{split} s_{i+1} &\geq \frac{2B + r_i N}{b} \\ \\ &= \frac{2B +2b s_{i-1} - 4B}{b} \\ \\ &= 2 s_{i-1} - \frac{2B}{b} \end{split}\]
So we get,
\[s_{i+1} \approx 2 s_{i-1} - \frac{2B}{b}\]
and since \(b \geq 2B\), we have that \(2B/b < 1\). Thus in general \(-2B/b\) is not influent in the final value and we can roughly say that
\[s_{i+1} \approx 2 s_{i-1}\]
The code for this optimization is
def bleichenbacher_opt_1(s, old_M):
global TOTAL_REQUESTS
fst = old_M.pop()
old_M.add(fst)
a = fst[0]
b = fst[1]
r = ceil((b * s - B2) * 2, N)
while True:
low_bound = ceil((B2 + r * N), b)
high_bound = ceil((B3-1 + r * N), a) + 1
for s in range(low_bound, high_bound):
new_ciphertext = (pow(s, E, N) * ENCRYPTED_FLAG) % N
str_hex = f"%0{PADDING_VALUE}x" % new_ciphertext
if oracle(str_hex):
return s
TOTAL_REQUESTS += 1
r += 1
#Further Optimizations
Throughout the years various other optimizations have been suggested to the basic functioning of the Bleichenbacher decryption algorithm. All of them try to tackle the following aspects of the algorithm:
-
Shorten the search-time for the next \(s_i\).
-
Shorten the computation to construct the intervals in \(M_i\).
I have somewhere the references to the various articles that optimized the attack. For now I'll just put the names of the optimizations:
- Tigher Bounds.
- Beta Method.
- Parallel Threads Methods.
- Skipping Holes.
- Trimmers.
#Final Code
By putting all the pieces of the puzzle together and by abstracting each step of the algorithm into its own functions that we showed previously, we get the following nice and simple algorithm
s = ceil(N, B3)
M = set([ (B2, B3 - 1) ])
while True:
if len(M) > 1 or TOTAL_REQUESTS == 0:
s = bleichenbacher_step_1(s)
else:
interval = M.pop()
if interval[0] == interval[1]:
print(f"Found result: {interval[0]}")
break
else:
M.add(interval)
s = bleichenbacher_opt_1(s, M)
M = bleichenbacher_step_2(s, M)
This is barely \(20\) lines of code.
#The Missing Step
At the start we assumed that the original plaintext \(m\) was correctly padded according to PKCS #1 v1.5.
What if that's not the case?
What if we catch a general encrypted message \(c\) and we want to decrypt it, even though the plaintext \(m\) is not PKCS compliant?
The attack can still be done, but before starting we need to find an \(s_0\) value such that \(c \cdot s_0^e \mod N\) is accepted by the oracle. To find this value we just generate \(s_0\) randomly and check the oracle.
-
If its valid, we let \(c^{'} = c \cdot s_0^e \mod N\) and start to execute the decryption algorithm on \(c^{'}\) as we did before.
-
If its not valid, we generate another \(s_0\) and try again.
#Connection to TLS
So far I did not talk about TLS because I did not want to introduce TLS complexities into the mix. It is important to mention however that this attack was first discovered in some SSLv3.0 implementations.
During the TLS handshake, which is the initial part of the protocol where sesison secrets are established. During the handshake many things happens. For example, the client can choose to authenticate the server, and vice versa, using X.509 certificates and the Public Key Infrastructure (PKI). Another thing that happen is that at some point a key is generated and shared between client and server. Once again, there are various methods for generating and sharing this key. Among these methods we find our culprit: RSA. In all but the latest TLS versions it is possible, assuming both client and server support the cipher, to exchange the generated symmetric key by using RSA encryption using PKCS#1v1.5 as padding scheme.
A fascinating aspect of this attack is its long history. Even though it was first discovered in \(1998\), researcher and standardizer at that time thought that they understood the issue and wrote within the official RFC documents possible remediations on how to fix the issue. The problem however did not disappear, and years later it kept resurfacing over and over again.
As more and more cases of such padding oracles were found, remediations kept getting harder and harder to write, implement and understand properly. In order to simplify the future and make it more robust, for the design of the latest version of the protocol, TLSv1.3, released in \(2018\), it was decided to completely remove the RSA+PKCS#1v1.5 option for the key exchange part of the protocol. A design choice which I respect and I'm grateful for.
By completely removing the option, it also automatically solved the problem of future Bleichenbacher's padding oracles. This shows that
Sometimes the best way to solve a problem is to make sure it cannot even exist in the first place
#Conclusion
I hope I was able to keep the topic interesting. If you have some feedback please let me know what you think of it, and also if you have some quesitons that I was not able to answer!
To finish off, I will link some useful references down below:
-
https://crypto.stanford.edu/~dabo/papers/RSA-survey.pdf
A survey done by Dan Boneh on the various attacks discovered on RSA.
-
https://blog.trailofbits.com/2019/07/08/fuck-rsa/
An article that explains other fragilities of RSA