Sometimes I look at things that already exist in the world and my eyes fill up with wonder and curiosity. I look at them and I ask myself: how did that thing come to exist exactly the way it is? Why was it done that way and not differently? I feel as if by answering those questions I get a little bit closer to those things, to the technology they represent and embody. And, by getting closer to the technology, in a way, I also get closer to a part of myself.
It saddnes me that in the context of computer science this point of view made of curiosity and wonder is most often negleted. Reflecting upon my personal experience studying computer science at university, especially during the first years, I felt very alienated by the fact that I had no idea regarding how most of the tools and technology I was using worked internally. Even at work, most of the time one is too busy developing new technology, that no time or resources are given to the simple yet foundamental act of rediscovering and reimplementing technologies that already exist.
Yet, I've always found an intrinsic value in the act of reinvent the wheel, so to speak. Because while it is true that the metaphorical wheel already exist, whatever it represents, it is also true that I did not build it, but someone else did. I believe that in building the wheel one gains much experience, not only about the specific technical work, but about life itself. Now, there are many ways of reinvent the wheel, but only one of them is always helpful, regardless of the context: that which comes out of a desire to learn and to play, and not to be too serious about it.
In this blog post I want to show how to build a wheel that has
already been built many times. A simple yet fascinating wheel that
has to do with base64 encoding and decoding. The wheel will be built
with the C programming language.
#What is base64?
First of all, what do we mean with "base64"?
When we talk about base64 we're essentially talking about an encoding scheme, which, roughly speaking, is a mechanism that allows us to assign to each character of a particular alphabet a specific number in such a way as to allow the translation from numbers to character and vice versa.
Example: The simplest type of assignment between characters and numbers we could imagine is the following one
\[\begin{split}
A &\longleftrightarrow 00 \longleftrightarrow 00000 \\
B &\longleftrightarrow 01 \longleftrightarrow 00001 \\
C &\longleftrightarrow 02 \longleftrightarrow 00010 \\
& \;\;\;\;\;\;\;\;\;\;\;\vdots \\\
\end{split}\]
The takeway here is that with an encoding we can transform characters into numbers, which can then be memorized in a computers memory as a sequence of bits. Viewed under this light, an encoding is the abstraction needed to make our computers deal with characters.
To specify an encoding one needs to specify two things:
-
The alphabet used.
-
The mapping between the characters in the alphabet and the associated numbers.
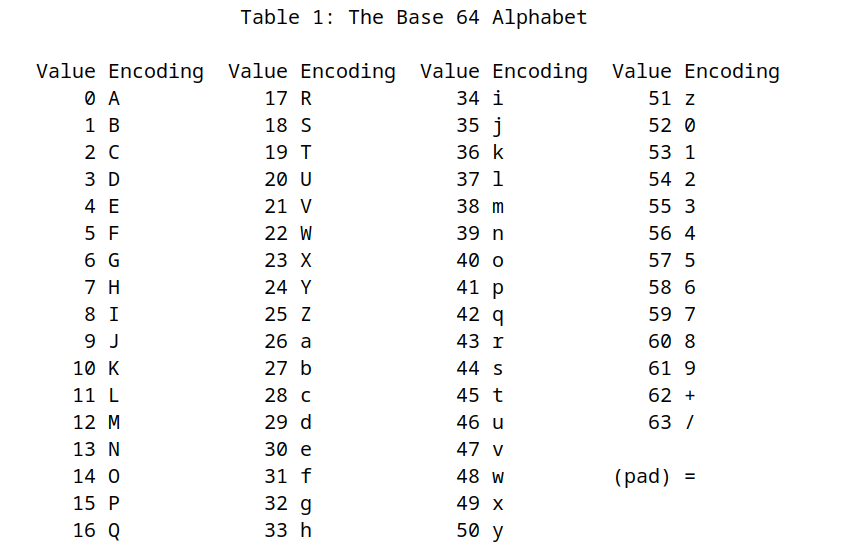
The base64 encoding, not so surprisingly, has an alphabet made up of \(64\) characters plus an extra padding character. The characters used are shown below.
abcdefghijklmnopqrstuvwxyz
ABCDEFGHIJKLMNOPQRSTUVWXYZ
0123456789
+/
= (extra padding character)
The specific mapping between characters and numbers can be analyzed in the original standardization of the encoding, which can be found in RFC4648.
In linux we have the base64 binary which allows for encoding and
decoding of arbitrary text.
which base64/usr/bin/base64echo "Hello World!" | base64SGVsbG8gV29ybGQhCg==echo "SGVsbG8gV29ybGQhCg==" | base64 -dHello World!
Our objective is to implement something similar to this: something that takes in input arbitrary bytes and produces as output the relative base64 encoding of those bytes. We're also interested in the decoding process, which goes from the base64 encoded bytes to the original bytes.
\[\begin{split} \text{Arbitrary Bytes} &\overset{\text{encoding}}{\longrightarrow} \text{Base64 bytes} \\ \\ \text{Arbitrary Bytes} &\overset{\text{decoding}}{\longleftarrow} \text{Base64 bytes} \\ \end{split}\]
#Why Base64?
Having discussed what do we mean exactly by base64, we can now ask the more difficult question: why do we need base64 encoding? What does it bring to the table?
The why questions are always the more important ones, especially before writing code. Why is it that people thought base64 was so needed that it had to be implemented and standardized? What kind of problem does it solve? Understanding the why is about understanding the bigger context in which that particular technology lives.
To understand the importance of base64 it is useful to remember
the concept of control characters, which sometimes are also called
non-printable characters. When we use our keyboard we typically
write out the characters that make up the alphabet of our natural
language, such as the latin characters abcdef... with their
upper-case counterparts ABCDEFG..., as well as the arabic numerals
we use to write out numbers 01234.... These characters are called
printable characters, because typically they are directly printed
by the programs that process them so that we can see them directly
on the screen. Now, along side printable characters there are
other characters, which, as it was mentioned earlier, are called
control charaters. These other kind of characters are special in
the sense that they do not represent any common written symbol,
but rather they are used to change the behavior of the program
that receives them.
The simplest example of a control character is the line feed,
which in most programming languages is represented with the
sequence of characters "\n". The actual byte value of the newline
is the hexadecimal byte 0x0a, which in decimal is the number
10. If we have a textual program, for example a program that
handles the graphics of a terminal, and such program reads the
byte 0x0a, then it will not print a specific character on the
screen. Rather, it will insert a newline, so that later characters
will be printed on the next line of the prompt.
This is exactly what happens with the echo command. When we
execute something with echo, the last character that is printed by
the program is a newline character (0x0a) and this is why that is
printed immediately after is printend in a newline, on its
own. This behavior can be analyzed with hexdump.
echo "Hello World!"Hello World!echo "Hello World!" | hexdump -C00000000 48 65 6c 6c 6f 20 57 6f 72 6c 64 21 0a |Hello World!.| 0000000d
If we instead do not want a newline to be printed at the end, we
can use the flag -n. If we once again anylze the bytes printed by
the command, we can see that now there is no newline. This means
that the terminal program will print the characters of the new
prompt immediately after the ! character.
echo -n "Hello World!" | hexdump -C
00000000 48 65 6c 6c 6f 20 57 6f 72 6c 64 21 |Hello World!|
0000000c
Now, remember the output alphabet used by base64. It is made up of all characters which, in the basic ascii encoding, are all printable characters. And now we're able to answer the question: why base64?
The idea behind base64 encoding is to take an arbitrary stream of bytes, which could contain control characters and normal non-control characters, and convert such sequence into a sequence made up of only normal non-control characters. This encoding process has to be done without losing any information about the original sequence of bytes, so that we can always go back and decode to obtain the original bytes.
The value behind base64 encoding is that it allows the transfering of arbitrary data without worrying about how the program that is receving the data will process it. In particular, by encoding all characters using printable, non control characters, we make sure that the receving program will not interpret the incoming data as control characters and therefore it will not change its behavior in unpexpected ways. Once the data has been received, the program can then choose what to do about it.
Having introduced the proper what/s and the proper why/s we're now able to describe the two main procedures we need to implement:
-
The base64 encoding process, which goes from arbitrary bytes to base64 bytes.
\[\text{Base64Encode}(\text{RawData}) \longrightarrow \text{Base64Data}\]
-
The base64 decoding process, which goes from base64 bytes to the original bytes.
\[\text{Base64Decode}(\text{Base64Data}) \longrightarrow \text{RawData}\]
These two produces are related in the sense that whathever it is encoded by the encoding procedure, must be correctly decoded by the decoding procedure in order to obtain the original bytes.
\[\text{Base64Decode}(\text{Base64Encode}(\text{RawData})) \longrightarrow \text{RawData}\]
#base64_encode()
Let us now describe the encoding procedure. Before showing the
actual code we will describe how to manually encode the string
"Hello World!" in base64.
To start off, remember that the ascii encoding tells us that each character of such sequence is a byte, and each byte is a number between \(0\) and \(255\). These numbers can be represented in various notation, such as hexadecimal notation or binary notation.
H -> 0x48 -> 01001000
e -> 0x65 -> 01100101
l -> 0x6C -> 01101100
l -> 0x6C -> 01101100
o -> 0x6F -> 01101111
-> 0x20 -> 00100000
W -> 0x57 -> 01010111
o -> 0x6F -> 01101111
r -> 0x72 -> 01110010
l -> 0x6C -> 01101100
d -> 0x64 -> 01100100
! -> 0x21 -> 00100001
Now, the main idea behind encoding in base64 is to consider the sequence of characters as a stream of bytes, each of which is made up of \(8\) bits. We want to split up this sequence in \(6\) bits blocks instead of the original \(8\) bit blocks. This means, essentially, that every \(3\) blocks of \(8\) bits we will have \(4\) blocks of \(6\) bits, since
\[3 \cdot 8 = 24 = 4 \cdot 6\]
Consider the first three bytes.
01001000 01100101 01101100
Let's split them in four blocks of six bits each.
010010 000110 010101 101100
The split is done simply by going from left to right and taking each time blocks of six bits. Sometimes we have to append bits taken from different bytes, but we always do it from left to right. And now, once we have all blocks of \(6\) bits, we extract from each of these block a character by taking the numerical value (written in base \(10\)) of each block and by using the previously shown base64 encoding table. In particular we have
010010 -> 18 -> S
000110 -> 6 -> G
010101 -> 21 -> V
101100 -> 44 -> s
And this means that the first four characters in the base64
encoding of our string will be SGVs. We can now decode the rest.
-
First, we consider all the remaining sequence of eight bit blocks
01101100 01101111 00100000 01010111 01101111 01110010 01101100 01100100 00100001 -
Then, for each three block of eight bit each we transform them into four block of six bit each.
01101100 01101111 00100000 -> 011011 000110 111100 100000 01010111 01101111 01110010 -> 010101 110110 111101 110010 01101100 01100100 00100001 -> 011011 000110 010000 100001 -
Then we transform each six bit block into character by using the base64 encoding table
011011 -> 27 -> b 000110 -> 6 -> G 111100 -> 60 -> 8 100000 -> 32 -> g 010101 -> 21 -> V 110110 -> 54 -> 2 111101 -> 61 -> 9 110010 -> 50 -> y 011011 -> 27 -> b 000110 -> 6 -> G 010000 -> 16 -> Q 100001 -> 33 -> h
Putting it all together, we obtain the following SGVsbG8gV29ybGQh.
\[\text{Hello World!} \longrightarrow \text{SGVsbG8gV29ybGQh}\]
which the same thing we obtain using the official binary base64
echo -n "Hello World!" | base64SGVsbG8gV29ybGQh
The procedure we described works perfectly everytime we have a number of characters which is an even multiple of \(3\). In this case our string had \(12 = 3 \cdot 4\) characters, which is why in the end we obtained an encoded string made up of \(16\) characters. What happens when this is not the case? What happens when we want to encode a string who's length is not an even multiple of \(3\)?
Notice we have two cases left to handle, depending if the length of our string, when divided by \(3\), has a remainder of \(1\) or \(2\). These cases will be called padding cases.
-
Padding case n.1: This case happens when we have a remainder of \(1\). The simplest case of this example is when we want to encode the string "
a". What we do in this case is that we use the first byte to extract two blocks of six bit each, which will represent two characters of the encoded base64 output, while the remaining two characters are filled with the padding character=.a -> 01100001 -> 011000 01 -> 011000 -> 24 -> Y 010000 -> 16 -> QNotice the way we use the final 2 bits of the initial byte. We use them to fill a block of six bit each by filling the remaining bits as zero bits. At the end the output we get is
YQ==as the base64 encoded output.echo -n "a" | base64YQ== -
Padding case n.2: This case is similar to the previous one, but this time we're able to use more bytes of the original input and we only need to use a single padding character
=. The simplest case is when we want to encode the string "aa".aa -> 01100001 01100001 -> 011000 010110 0001 -> 011000 -> 24 -> Y 010110 -> 22 -> W 000100 -> 4 -> EAt the end we get
YWE=as the base64 encoded output.echo -n "aa" | base64YWE=
Having done a manual example, which is always important to do the first time around, we're now able to write the code of interest. In particular we will write a function with the following signature
void base64_encode(const char *in, const unsigned long in_len, char *out);
We are given three arguments in input, the in pointer, which points
to the input string, the arbitrary sequence of bytes we want to
encode, the in_len which represents the length of the input, and,
finally, the out pointer, which points to a memory region which we
assume has already been allocated with the enough length in order
to contain the entire base64 of the input.
We will also use the following string, which encodes the base64 conversion table, going from numbers to characters in the base64 charset.
char *BASE64 = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/";
As we can see, when we do BASE64[x] we're getting the character
corresponding to the numerical value x. Of course we have that 0 <= x <= 63.
The implementation then is pretty straight-forward. The only thing that could take a bit of time to understand is the usage of the bit and shift operators.
void base64_encode(const char *in, const unsigned long in_len, char *out) {
int in_index = 0;
int out_index = 0;
while (in_index < in_len) {
// process group of 24 bit
// first 6-bit
out[out_index++] = BASE64[ (in[in_index] & 0xFC) >> 2 ];
if ((in_index + 1) == in_len) {
// padding case n.1
//
// Remaining bits to process are the right-most 2 bit of on the
// last byte of input. we also need to add two bytes of padding
out[out_index++] = BASE64[ ((in[in_index] & 0x3) << 4) ];
out[out_index++] = '=';
out[out_index++] = '=';
break;
}
// second 6-bit
out[out_index++] = BASE64[ ((in[in_index] & 0x3) << 4) | ((in[in_index+1] & 0xF0) >> 4) ];
if ((in_index + 2) == in_len) {
// padding case n.2
//
// Remaining bits to process are the right most 4 bit on the
// last byte of input. We also need to add a single byte of
// padding.
out[out_index++] = BASE64[ ((in[in_index + 1] & 0xF) << 2) ];
out[out_index++] = '=';
break;
}
// third 6-bit
out[out_index++] = BASE64[ ((in[in_index + 1] & 0xF) << 2) | ((in[in_index + 2] & 0xC0) >> 6) ];
// fourth 6-bit
out[out_index++] = BASE64[ in[in_index + 2] & 0x3F ];
in_index += 3;
}
out[out_index] = '\0';
return;
}
Let's consider for example how we compute the second block of six bits. The relative code is the following
// second 6-bit
out[out_index++] = BASE64[ ((in[in_index] & 0x3) << 4) | ((in[in_index+1] & 0xF0) >> 4) ];
In this line we're encoding the operation of taking the two right
most bit of the first byte and concatenating them with the four
left most bit of the second byte. The masks here are used to
extract these sequence of bits from the original number, and the
shift operations are used to place correctly the bits. Finally, the
OR operation is used to combine the two sequences of bits in order
to obtain the final and correct value. This value is then used as
an index into the BASE64 array, which gives us the corresponding
base64 character.
Consider the following two bytes
in[in_index] -> 01001000
in[in_index + 1] -> 01100101
We can break the previous computation into single steps as follows
(in[in_index] & 0x3) -> 01001000 & 00000011 -> 00000000
(in[in_index] & 0x3) << 4 -> 00000000 << 4 -> 00000000
(in[in_index+1] & 0xF0) -> 01100101 & 11110000 -> 01100000
(in[in_index+1] & 0xF0) >> 4 -> 01100000 >> 4 -> 00000110
Putting it all together we get
((in[in_index] & 0x3) << 4) | ((in[in_index+1] & 0xF0) >> 4)
-> 00000000 | 00000110
-> 00000110
-> 6
And therefore we obtain
BASE64[ 6 ] -> G
#base64_decode()
Having discussed the encoding procedure, we can now discuss the decoding procedure. This time we start from a sequence of bytes which have been obtained by following the base64 encoding procedure, and we want to extract the original sequence of bytes. As before, I will first show how to execute manually the algorithm, and then I will show the relative code.
Consider the string "SGVsbG8gV29ybGQh" we obtained in the previous
step. We now want to decode it and obtain the original string.
To start off, there is already something we can immediately to in order to check if the string we're trying to decode is a valid base64 string. The idea is that the length of all valid base64 sequences must be a multiple of \(4\). In our case we have
\[\text{Length}(\text{SGVsbG8gV29ybGQh}) = 16\]
First we consider the ascii encoding for all characters of the base64 string. The idea behind base64 decoding is to start from the ascii encoding value of the various base64 characters and reconstruct the relative six bit value that was computed during the encoding process. This can be done by connecting the numbers between the ascii encoding table and the base64 encoding table.
For example, consider the character S. In ascii encoding S is
mapped to the hexadecimal number 0x53, which in decimal is 83. In
the base64 encoding table however S is mapped to the number
18. This creates the following mapping between 0x53 and 18.
(ascii) (base64)
0x53 <---------> S <---------> 18
We do this for all characters of the original string in order to obtain the relative six bit value that was found during the encoding process.
S -> 0x53 -> 18 -> 010010
G -> 0x47 -> 6 -> 000110
V -> 0x56 -> 21 -> 010101
s -> 0x73 -> 44 -> 101100
b -> 0x62 -> 27 -> 011011
G -> 0x47 -> 6 -> 000110
8 -> 0x38 -> 60 -> 111100
g -> 0x67 -> 32 -> 100000
V -> 0x56 -> 21 -> 010101
2 -> 0x32 -> 54 -> 110110
9 -> 0x39 -> 61 -> 111101
y -> 0x79 -> 50 -> 110010
b -> 0x62 -> 27 -> 011011
G -> 0x47 -> 6 -> 000110
Q -> 0x51 -> 16 -> 010000
h -> 0x68 -> 33 -> 100001
Now we can combine sequences groups of four six bit blocks into sequences of three eight bit blocks.
010010 000110 010101 101100 -> 010010 00|0110 0101|01 101100
-> 01001000 01100101 01101100
And from each of these byte we can use the ascii encoding to get back the original value.
01001000 -> 72 -> H
01100101 -> 101 -> e
01101100 -> 108 -> l
The first three bytes of the original output are Hel. We can do
the same procedure for all remaining bytes.
011011 000110 111100 100000 -> 011011 00|0110 1111|00 100000
->
-> 01101100 -> l
01101111 -> o
00100000 -> ' '
010101 110110 111101 110010 -> 010101 11|0110 1111|01 110010
->
-> 01010111 -> W
01101111 -> o
01110010 -> r
011011 000110 010000 100001 -> 011011 00|0110 0100|00 100001
->
-> 01101100 -> l
01100100 -> d
00100001 -> !
At the end we obtain the string "Hello World!", which is the
correct one.
\[\text{SGVsbG8gV29ybGQh} \longrightarrow \text{Hello World!}\]
In terms of code, we define the following signature.
int base64_decode(const char *in, const unsigned long in_len, char *out);
The meaning of the various arguments is essentially the same as the encoding procedure, only that now the input is a base64 encoded string, while the output can be an arbitrary sequence of bytes. Once again, we assume that the output has already been allocated with the proper length.
To actually implement the decoding procedure we need to define a translation table which allows us to obtain the base64 numerical code of the various characters, that is, the numerical value of the various characters defined in the base64 table. The table is defined as follows
// This table implements the mapping from 8-bit ascii value to 6-bit
// base64 value and it is used during the base64 decoding
// process. Since not all 8-bit values are used, some of them are
// mapped to -1, meaning that there is no 6-bit value associated with
// that 8-bit value.
//
int UNBASE64[] = {
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, // 0-11
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, // 12-23
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, // 24-35
-1, -1, -1, -1, -1, -1, -1, 62, -1, -1, -1, 63, // 36-47
52, 53, 54, 55, 56, 57, 58, 59, 60, 61, -1, -2, // 48-59
-1, 0, -1, -1, -1, 0, 1, 2, 3, 4, 5, 6, // 60-71
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, // 72-83
19, 20, 21, 22, 23, 24, 25, -1, -1, -1, -1, -1, // 84-95
-1, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, // 96-107
37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, // 108-119
49, 50, 51, -1, -1, -1, -1, -1, -1, -1, -1, -1, // 120-131
};
We have for example that UNBASE64[84] = 19 because in ascii
encoding the decimal value 84 represent the character T, which, in
the base64 table, is mapped to the number 19.
We are now ready too see the entire code for the decoding process.
int base64_decode(const char *in, const unsigned long in_len, char *out) {
int in_index = 0;
int out_index = 0;
char first, second, third, fourth;
assert(!(in_len & 0x03)); // input must be even multiple of 4
while( in_index < in_len ) {
// check if next 4 byte of input is valid base64
for (int i = 0; i < 4; i++) {
if (((int)in[in_index + i] > 131) || UNBASE64[ (int) in[in_index + i] ] == -1) {
fprintf(stderr, "Invalid base64 char, cannot decode: %c\n", in[in_index + i]);
return -1;
}
}
// extract all bits and reconstruct original bytes
first = UNBASE64[ (int) in[in_index] ];
second = UNBASE64[ (int) in[in_index + 1] ];
third = UNBASE64[ (int) in[in_index + 2] ];
fourth = UNBASE64[ (int) in[in_index + 3] ];
// reconstruct first byte
out[out_index++] = (first << 2) | ((second & 0x30) >> 4);
// reconstruct second byte
if (in[in_index + 2] != '=') {
out[out_index++] = ((second & 0xF) << 4) | ((third & 0x3C) >> 2);
}
// reconstruct third byte
if (in[in_index + 3] != '=') {
out[out_index++] = ((third & 0x3) << 6) | fourth;
}
in_index += 4;
}
out[out_index] = '\0';
return 0;
}
The workings of the code should now be clear. First we check if the input is an even multiple of \(4\), and then we iterate over all the blocks. At each iteration we transform a consecutive sequence of four blocks into three bytes of the output. To perform this transformation we first unbase the values to obtain the actual six bit values, and then we combine the six bit values in order to obtain the original eight bit values.
#Conclusion
Not much to say anymore, other than I hope it was an interesting and fun read. Have fun in your projects, and do not be afraid of trying to "reinvent the wheel", because learning something new is always a magical thing, regardless of how many times in the past it has already been done by other humans.